In this problem, we will prove that equal chords have equal arcs. This is true for equal chords in a single circle, and for chords in two circles with the same radius. We will also show that the converse is true- if the arcs are equal, the chords will be equal.
Problem
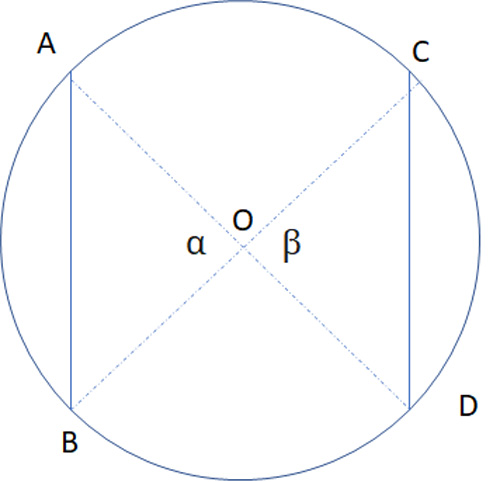
In circle O, chords AB and CD are equal - |AB|=|CD|. Show that the arcs that subtend these chords are equal.
Strategy
Arcs are defined by the central angle of the circle that subtends it. So to show that the two arcs are equal, we will need to show their two central angles, α and β, are congruent.
To show that two angles are congruent, we can use congruent triangles, where these angles are corresponding angles, and where the equal chords are corresponding sides.
When looking for congruent triangles in a circle, it is useful to see if we can make the radii of a circle the sides of those triangles, since all radii are equal.
And now the solution presents itself: triangles △OAB and △OCD are congruent by the Side-Side-Side postulate (one side is the equal chord, the other two sides are radii, which are equal). So α≅β as corresponding parts of congruent triangles, and then by definition, arc AB is equal to arc CD.
Proof
(1) |AB|=|CD| //given
(2) |OA|=|OC|= r //all radii of a circle are equal
(3) |OB|=|OD|= r //all radii of a circle are equal
(4) △OAB ≅△OCD //(1), (2), (3), Side-Side-Side postulate
(5) α≅β //(4) Corresponding angles of congruent triangles (CPCTC)
(6) Arc(AB)=Arc(CD) //(5), definition of equal arcs
Converse theorem
Having proven the theorem, let's now quickly show that the converse is also true- if we have equal arcs, the corresponding chords will be equal.
We will follow the same strategy as above, showing the triangles formed by the chords and the radii are congruent. And to do that, we will simply replace the equal chord with the equal arc. If the arcs are equal, then by definition so are their central angles, and the triangles are congruent by the Side-Angle-Side postulate. And as a result, the chords are equal as corresponding sides in congruent triangles.
Proof of the converse theorem
(1) Arc(AB)=Arc(CD) //given
(2) α≅β //(1) Definition of equal arcs
(3) |OA|=|OC|= r //all radii of a circle are equal
(4) |OB|=|OD|= r //all radii of a circle are equal
(5) △OAB ≅△OCD //(2), (3), (4), Side-Angle-Side postulate
(6) |AB|=|CD| //(5), Corresponding sidesof congruent triangles (CPCTC)
