Circles
In geometry, a circle is defined as the collection of all points that are the same distance from one point, which is the center of the circle.
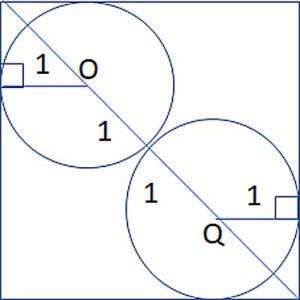
The distance from the center of the circle to any point on the circle is called the radius, and commonly written 'r'.
If we draw a line from one point on the circle, through its center and on to another point on the circle, directly across from the first point, that line's length will be 2 times r, and is called the circle's diameter, 'd'. d= 2*r
A circle is a geometric shape completely defined by its radius- knowing the radius we can calculate the circle's area, and its circumference.
A circle's circumference, C, is Ccircle=2*π*r (where r is the radius) , and since the diameter, d, is 2 times r, we can also write Ccircle=d*π
A circle's area is given by the formula Acircle=π*r2
--
Now that we've explained the basic concept of circles in geometry, let's scroll down to work on specific geometry problems relating to this topic.