In today's lesson, we will show that a line connecting the centers of two intersecting circles is a perpendicular bisector of the common chord of the two circles, connecting the intersection points.
When two circles intersect, we can connect the two intersection points and create a common chord.
If we connect the centers of these two circles, the connecting line will be a perpendicular bisector of the common chord, as we will now show.
Problem
Circles O and Q intersect at points A and B. Show that the line OQ connecting the centers of the two circles bisects AB and is perpendicular to AB.
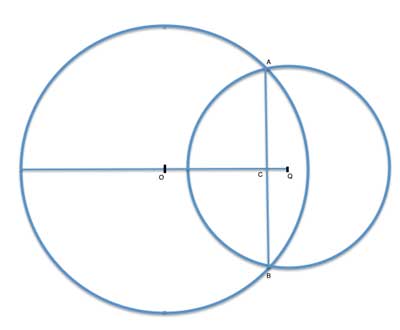
Strategy
Many problems involving circles and chords make use of the fact that all of a circle's radii are equal, and use this fact to show congruent triangles, so let's draw those radii:

This immediately suggests we could solve this geometry problem by first showing that triangles △AOQ and △BOQ are congruent (using the Side-Side-side postulate - We've actually already done that as an exercise here - Congruent Triangles in a Circle ).
And after doing that, we could easily show that triangles △AOC and △BOC are congruent using the Side-Angle-Side postulate, having just shown that ∠AOC is congruent to ∠BOC as corresponding angles in the congruent triangles △AOQ and △BOQ).
But there's an even easier way. The radii of each circle are equal, OA=OB and QA=QB, which means that OAQB is a kite (just like it looks in the diagram!). And we know that in a kite, the diagonal connecting the corners between the equal sides bisects the other diagonal. We also know that the diagonals are perpendicular to each other. So we are done!
Proof
(1) OA=OB //radii of a circle are equal
(2) QA=QB //radii of a circle are equal
(3) OAQB is a kite //(1) , (2) , definition of a kite
(4) AC=CB // (3), diagonal connecting the angles formed by the equal sides bisects the other diagonal
(5) AB⊥OQ // (3), diagonals of a kite are perpendicular
