Inscribed Shapes

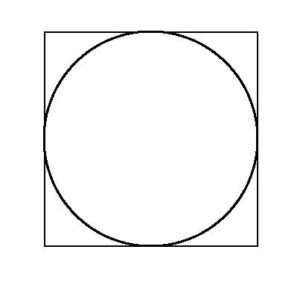
Many geometry problems deal with shapes inside other shapes. For example, circles within triangles or squares within circles.

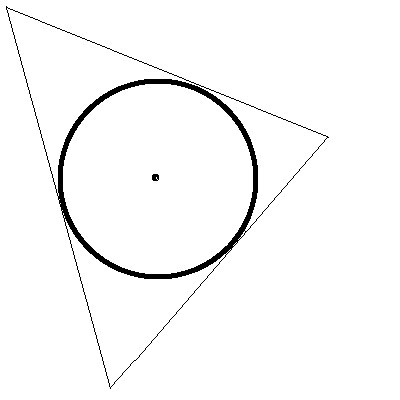
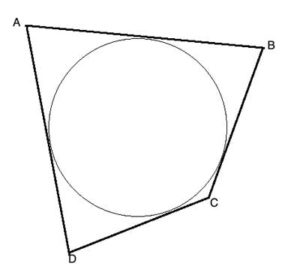
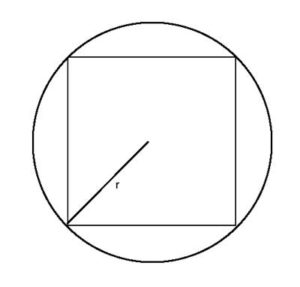
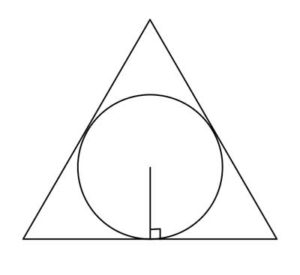
The inner shape is called "inscribed," and the outer shape is called "circumscribed."

When a circle is inscribed inside a polygon, the edges of the polygon are tangent to the circle.

--
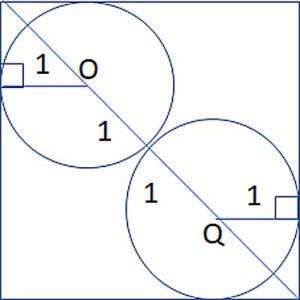
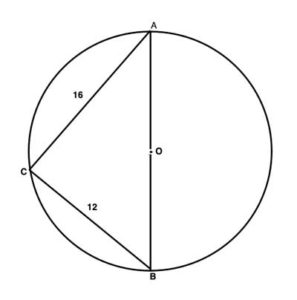
Now that we've explained the basic concept of inscribed shapes in geometry, let's scroll down to work on specific geometry problems relating to this topic.