Kites (Deltoids)

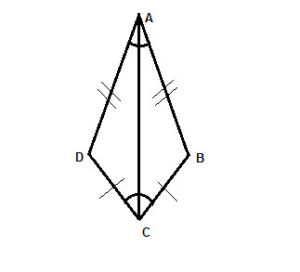
A kite, also called a deltoid, is a quadrilateral in which there are two pairs of adjacent edges that are equal.

The diagonals of a kite are perpendicular to each other.

The diagonal which connects the two corners between the equal edges (which is the kite's axis of symmetry) bisects the angles at its endpoints, and bisects the other diagonal.

The other diagonal - which connects corners between unequal edges - does not bisect the angles at its endpoints, but splits the deltoid into two isosceles triangles.

The angles between the unequal edges are congruent.

We will prove these kite properties using triangle congruence.

--
Now that we've explained the basic concept of kites in geometry, let's scroll down to work on specific geometry problems relating to this topic.