Quadrangles
Quadrangles (also called quadrilaterals) are polygons with 4 edges, and 4 angles, or vertices, at the corners.
Special quadrangles
There are several types of special polygons, with unique properties that depend on factors such as:
1. If their sides are parallel to each other or not - and if they are parallel, are both pairs of opposite edges parallel, or just one set
2. If their sides are all equal or if they just have two pairs of equal sides.
3. If the angles are right angles.
And more.
We have a section for each special type of polygon, describing and proving their properties, which are very common in high school geometry problems.
The sum of the angles in a quadrangle
One property that is common to all quadrangles, other than 4 sides and 4 vertices, is that the sum of the angles in a quadrangle is always 360°. The proof of this is simple.
Proof: Show that the sum of interior angles in a simple convex quadrangle is always 360°
Let’s think about the strategy to do this. 360 is a familiar number - it is the measure of angles in a circle, but there are no circles here, so let’s rule that out.
360 is also 2x180, and that is also a familiar number – it is the sum of the angles in a triangle – so, if we can show that this quadrangle is composed of two triangles we will have the proof- and that’s all we need.
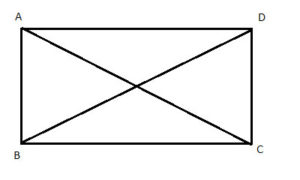
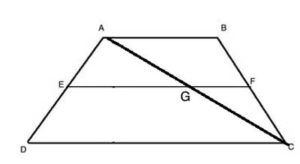
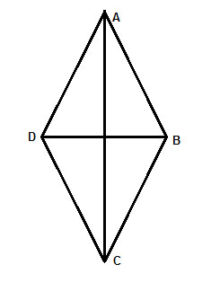
Proof: In any simple convex polygon, a line connecting 2 points on the perimeter of the polygon is entirely within the polygon, per the definition of convex polygons. So, let’s draw a line connecting two opposite corners of the quadrangle (such a line is a called a ‘diagonal’) – say from C to A:
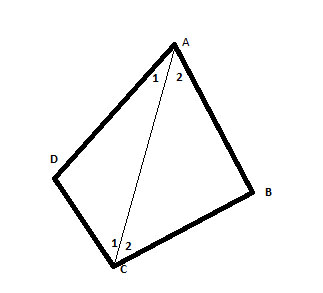
(1) m∠A1 + m∠D+ m∠C1 = 180° //sum of the interior angles in triangle ΔADC
(2) m∠A2 + m∠B+ m∠C2 = 180° //sum of the interior angles in triangle ΔABC
(3) m∠A1 + m∠D+ m∠C1+m∠A2 + m∠B+ m∠C2 = 360° //add both equations
(4) m∠A1 + m∠A2 +m∠D+ m∠C1+ m∠C2 + m∠B= 360° //re-arrange terms
(5) m∠A1 + m∠A2 = m∠A // angle addition postulate
(6) m∠C1 + m∠C2 = m∠C // angle addition postulate
(7) m∠A+m∠D+ m∠C + m∠B= 360° ∎ //substitution property of equality
--
Now that we've explained the basic concept of quadrangles in geometry, let's scroll down to work on specific geometry problems relating to this topic.