The Diagonals Divide a Parallelogram Into Four Equal Areas

In today's lesson, we will prove that the interacting diagonals of a parallelogram divide it into four triangles, all of which have equal areas.

Each of the diagonals of a parallelogram divides it into two congruent triangles, as we saw when we proved properties like that the opposite sides are equal to each other or that the two pairs of opposite angles are congruent. Since those two triangles are congruent, their areas are equal.

We also saw that the diagonals of the parallelogram bisect each other, and so create two additional pairs of congruent triangles.

Now will go one step further, and relying on the fact that triangles with the same base and same height have equal areas, we will see that all four triangles created by the intersecting diagonals of a parallelogram have equal areas.

Problem

ABCD is a parallelogram with diagonals AC and BD which intersect at point O. Show that all four triangles created by these diagonals - ΔAOD,  ΔCOD, ΔAOB and  ΔCOB - have equal areas.

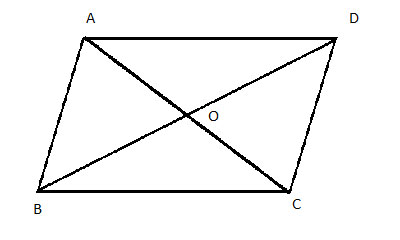
Strategy

We already know that the opposite pairs of triangles (ΔAOD≅ ΔCOB; ΔAOB≅ ΔCOD) are congruent, and thus have equal areas. So if we can show that one of the other pairs also has equal areas, all four will be equal.

When comparing the ratio of areas of triangles, we often look for an equal base or an equal height - in this case, we have both: Since the diagonals bisect each other, AO=OC, and both ΔCOB and ΔAOB share the same height - BE.

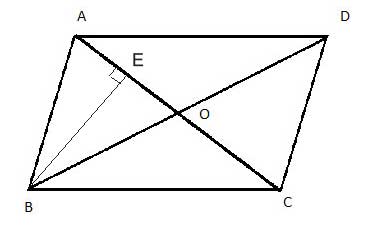
So their areas are equal, and so all four areas are equal.

Proof

First, we'll repeat the proof that the 2 opposite pairs of triangles are congruent:

(1) ABCD is a parallelogram    //Given
(2) AD || BC                                 //From the definition of a parallelogram
(3) AD = BC                                 //Opposite sides of a parallelogram are equal in size
(4) ∠OBC ≅ ∠ODA                      //Alternate Interior Angles Theorem
(5) ∠OCB ≅ ∠OAD                      //Alternate Interior Angles Theorem
(6) ΔOBC ≅ ΔODA                      // (3), (4), (5), Angle-Side-Angle
(7) BO=OD                                // Corresponding sides in congruent triangles (CPCTC)
(8) AO=OC                                // Corresponding sides in congruent triangles (CPCTC)
(9) AB=DC //Opposite sides of a parallelogram are equal in size
(10) ΔAOB ≅ ΔCOD                 // (7), (8), (9), Side-Side-Side

Now let's look at the areas of these triangles:
(11) Area_ΔOBC = Area_ΔODA //(6), congruent triangles have equal areas
(12) Area_ΔAOB = Area_ΔCOD //(10), congruent triangles have equal areas
(13) Area_ΔAOB =BE·AO/2 //Area of triangle
(14) Area_ΔOBC =BE·OC/2 //Area of triangle
(15) Area_ΔOBC = Area_ΔAOB //(13), (14), (8) , triangles with equal bases and heights.
(16) Area_ΔOBC = Area_ΔAOB=Area_ΔODA = Area_ΔCOD