In today's lesson, we will prove the alternate interior theorem, stating that interior alternating angles and exterior alternating angles between parallel lines are congruent.
Prove:
Interior alternating angles and exterior alternating angles are congruent (that is, they have the same measure of the angle.)
How to approach this problem?
So how do we go about this? We’ve already proven a theorem about 2 sets of angles that are congruent. So we will try to use that here, since here we also need to prove that two angles are congruent.
So let’s proceed to the proof, using what we already know about corresponding angles formed by a transverse line and two parallel lines, and the theorem we’ve already proven.
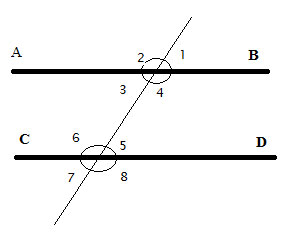
Problem
AB||CD, prove m∠5 = m∠3 , and that m∠1 = m∠7
Proof
Here's how you prove the alternate interior angles theorem:
(1) AB||CD //given
(2) ∠1 ≅ ∠5 //from the axiom of parallel lines – corresponding angles
(3) m∠1 = m∠5 //definition of congruent angles
(4) m∠1 = m∠3 //vertical, or opposite angles
(5) m∠5 = m∠3 //using (3) and (4) and transitive property of equality, both equal m∠1
And in a similar way,
(1) AB||CD //given
(2) ∠1 ≅ ∠5 //from the axiom of parallel lines – corresponding angles
(3) m∠1 = m∠5 //definition of congruent angles
(4) m∠5 = m∠7 // vertical, or opposite angles
(5) m∠1 = m∠7 //using (3) and (4) and transitive property of equality, both equal m∠5
The converse of this theorem is also true, that is, if m∠5 = m∠3 , or if m∠1 = m∠7 , then AB||CD.