In today's geometry lesson, we'll prove the converse of the Alternate Interior Angles Theorem.
We have shown that when two parallel lines are intersected by a transversal line, the interior alternating angles and exterior alternating angles are congruent (that is, they have the same measure of the angle.)
We will now show that the opposite is also true. If the interior alternating angles or exterior alternating angles created by the transversal line are congruent, then the two lines intersected by the transversal line are parallel.
Problem
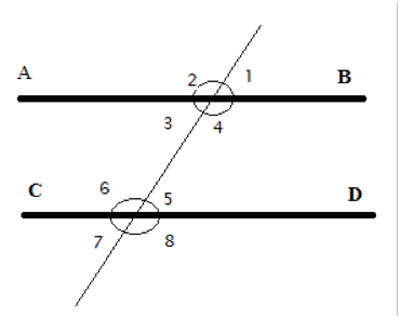
Given m∠5 = m∠3 or m∠1 = m∠7 , prove that AB||CD
Strategy
To prove two lines are parallel, we can use the converse of the Corresponding Angles Theorem - if we find a pair of corresponding angles that are congruent, then the two lines are parallel.
So let's do exactly what we did when we proved the Alternate Interior Angles Theorem, but in reverse - going from congruent alternate angles to showing congruent corresponding angles.
Proof
Here's how you prove the converse of the Alternate Interior Angles Theorem:
(1) m∠5 = m∠3 //given
(2) m∠1 = m∠3 //vertical, or opposite angles
(3) m∠1 = m∠5 //using (1) and (2) and transitive property of equality, both equal m∠3
(4) ∠1 ≅ ∠5 //(3), the definition of congruent angles
(5) AB||CD //converse of the Corresponding Angles Theorem
And similarly, for the exterior pair:
(1) m∠1 = m∠7 //given
(2) m∠5 = m∠7 //vertical, or opposite angles
(3) m∠1 = m∠5 //using (1) and (2) and transitive property of equality, both equal m∠7
(4) ∠1 ≅ ∠5 //(3), the definition of congruent angles
(5) AB||CD //converse of the Corresponding Angles Theorem