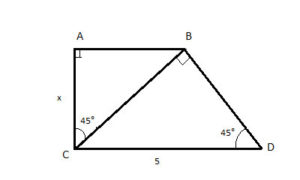
Right Triangles
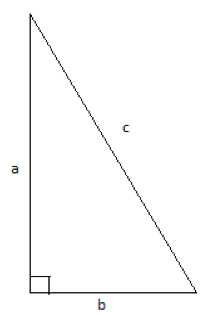
A triangle in which one of the edges is perpendicular to another, forming a 90° angle is called a “Right triangle”:
The two edges which form the right angle (a and b) are called the “legs”, and the third edge (c), opposite the right angle, is called the hypotenuse.
The properties of right triangles, which we will prove, are the things we will use in problems involving right triangles. These include:
1. The Pythagorean theorem: a2+b2 = c2 – this will be useful in any problem that asks us to find the edge lengths or areas of shapes made up of one or more right triangles.
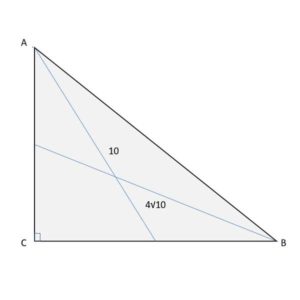
2. The length of the median – a line that connects a vertice (or corner) of a triangle to the mid-point of the opposite side – to the hypotenuse is equal to half the length of the hypotenuse. We will use this whenever we see the median in a problem or the mid-point of the hypotenuse being used.
3. The sum of the two angles that are not the right angle is 90° (since the sum of all the angles is 180 °, and the right angle is 90°, so the other two must sum up to 180°-90°= 90°). We’ll use these in problems involving finding angle sizes in right triangles.
--
Now that we've explained the basic concept of right triangles in geometry, let's scroll down to work on specific geometry problems relating to this topic.