Medians to Legs of a Right Triangle

Here we will use the lengths of the medians to legs of a right triangle to find the length of the hypotenuse and the length of the legs of the triangle. This will also enable us to find the length of the third median, and the triangle's area.

We will work first with a numerical example, and then derive a general formula.

Problem

The problem: Using medians to legs of a right triangle to find the 3rd median.

In a right triangle ΔABC, the median to one of the legs measures 10 units, and the other measures 4√10. Find the length of the third median.

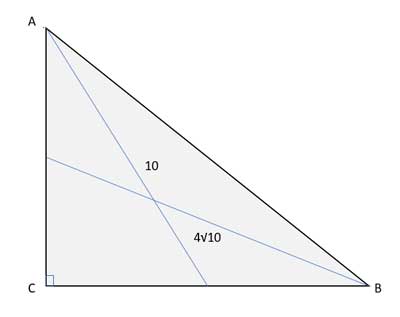
Strategy

In another problem, we saw that in a right triangle, the median to the hypotenuse is equal to half the hypotenuse. So, to find the third median (to the hypotenuse), we should first find the length of the hypotenuse.

To do that, let's refer to the drawing above, and note that the medians to the legs both form right triangles. Since they are medians, they split each of the legs into two equal parts. Let's label those "half legs" x and y, respectively:

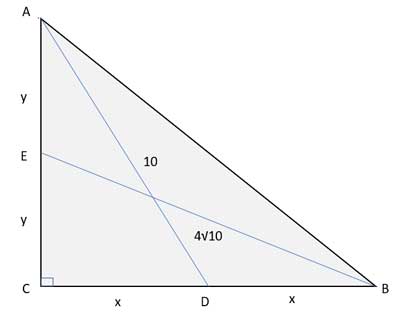
We'll use the Pythagorean theorem in both triangles (ΔADC and ΔEBC), and solve for x and y with a bit of algebra. Once we have x and y, we can use the Pythagorean theorem again, this time in ΔABC. With this, we'll find the length of the hypotenuse, and from it, the length of the third median.

Solution

(1) y²+(2x)²= (4√10)² //Pythagorean theorem applied to ΔEBC
(2) x²+(2y)²= 10² //Pythagorean theorem applied to ΔADC
(3) x²= 100- 4y² //rearranging (2)
(4) y²+4(100-4y²)= (4√10)² //substitute for x² from (3) into (1)
(5) 15y² = 240 //(4), simplify and rearrange
(6) y² =16
(7) y=4
(8) x²= 100- 64 //(7) , (3)
(9) x= 6
(10) |AC|=2y=8 // (7), BE is the median
(11) |CB|=2x=12 // (9), AD is the median
(12) |AB|²= 8²+12² //(10), (11) , Pythagorean theorem applied to ΔABC
(13) |AB|= √(64+144) = √208 = √(16⋅13)= 4√13

From this, the third median, which is the median to the hypotenuse, is 2√13, or half the hypotenuse.

General formula

Now that we've solved the specific numerical example, let's see if we can come up with a generic formula that uses the lengths of the medians to the legs to define the other median and the sides of ΔABC.

Let's first label the sides of ΔABC as a, b, and c (with c being the hypotenuse). We'll label the median to a as m_a. Likewise, we'll label the median to b as m_b and similarly, the median to the hypotenuse m_c.

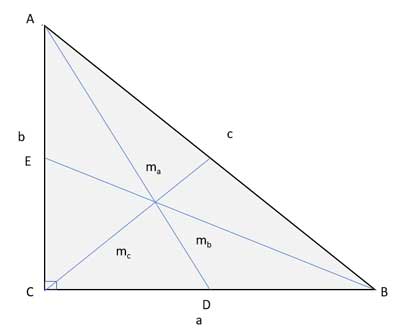
Applying the Pythagorean theorem to ΔEBC, m_b² = a² + b²/4.
And applying the Pythagorean theorem to ΔADC, m_a² = b² + a²/4.
Solving this system of equations, the same way as we did above in the numerical example we get:

a = 2√[(4m_b²-m_a²)/15]
b= 2√[(4m_a²-m_b²)/15]

Plugging this into the Pythagorean theorem for the main triangle, ΔABC, where we know c² = a²+b², we get c = 2√[(m_b²+m_a²)/5].

(You can plug in m_a=10 and m_b= 4√10 to confirm the numerical result we got above).

The third hypotenuse is then m_c=√[(m_b²+m_a²)/5] - half of c.

If we want a formula for the triangle's area- it is a⋅b/2, or 2/15√[(4m_a²-m_b²)(4m_b²-m_a²)]