Similar Triangles

Two triangles are said to be 'similar' if their corresponding angles are all congruent. Which means they all have the same measure.

This is different from congruent triangles because congruent triangles have the same length and the same angles. But two similar triangles can have the same angles, but with a different size of corresponding side lengths.

Think of it as "expanding" or "shrinking" a triangle by the same amount in all directions, keeping the proportions the same, but the sizes different:

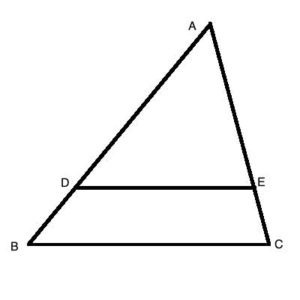
We denote similar  triangles using this symbol: ∼, for example:

ΔABC∼ ΔDEF

A key property of similar triangles is that their sides are all proportional with the same ratio, called the "scale factor". So if ΔABC∼ ΔDEF, and side AB is twice as large as side DE, this same scale factor of 2:1 holds for all the other sides as well: BC = 2*EF, AC = 2*DF.

We can write this as AB/DE=BC/EF=AC/DF=scale factor. From this, we can derive other relationships, like the product of multiplying two sides:

AB/DE = BC/EF, so if we cross-multiply we get

AB*EF = BC*DE

And, since we know from basic algebra that if a/b=c/d, then a/c=b/d, we also have AB/BC=DE/EF - so the relationship between two sides of of the triangles is the same as the relationship between those two corresponding triangles in the other similar triangle.

The scale factor also holds true for the triangles' height and perimeter. The areas, which are (base*height/2) is the scale factor squared, since we are multiplying two parts (the base and the height) and each one of them is scaled by the same factor.

 

--
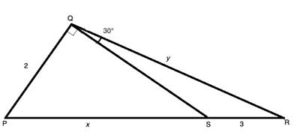
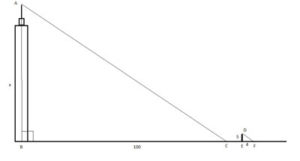
Now that we've explained the basic concept of similar triangles in geometry, let's scroll down to work on specific geometry problems relating to this topic.