One application of the properties of similar triangles is to find the height of very tall objects such as buildings using the length of their shadow on the ground and comparing it to the length of the shadow of a known object. These types of word problems are very common in high school geometry textbooks.
Strategy
The solution to this kind of problem relies on making a couple of assumptions and approximations, which are assumed to be true.
The first is that the sun is far enough from the Earth that we can assume the light rays are parallel to each other. The other is that the ground on which the shadow falls is flat and that the objects are
Often the problem statement will tell you to assume that they are true (and if not, you can note that you are making this assumption in your answer, just for completeness).
With these two assumptions, the two objects and their shadows form two similar triangles. Each has one right angle (between the object and its shadow on the ground) and one congruent angle which is a corresponding angle between two parallel lines (the Sun's rays) intersected by a transversal line - the ground:
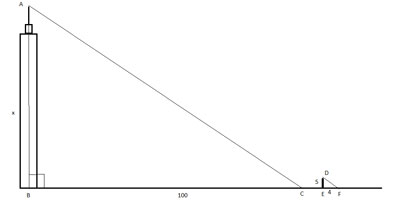
Problem
A tower casts a shadow on a flat football field which is 100 feet long. At the same time, a 5-foot long pole in the picket fence around the field casts a shadow that is 4 feet long. How tall is the tower?
Solution
How to calculate the height of tall objects: Draw the problem, as above, and show the triangles are similar. (we are told the ground is flat, and that the shadow measurements are made at the same time, so our assumptions are true)
(1) m∠ABC=m ∠DEF= 90° //Given
(2) ∠ABC ≅ ∠DEF // (1) , Definition of congruent angles
(3) AC||DF //Assumption, Sun's rays are parallel
(4) ∠ACB ≅ ∠DFE // Corresponding angles of parallel lines
(5) Δ ABC ~ Δ DEF // (2), (3), Angle-Angle
(6) AB/BC = DE/EF // Properties of similar triangles
(7) BC = 100 // Given
(8) DE = 5 // Given
(9) EF = 4 // Given
(10) x/100 = 5/4 //(5), (6),(7),(8), substitution
(11) x= 500/4=125
