Intersecting Lines and Angles

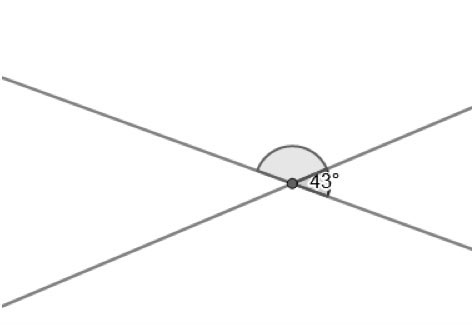
Two intersecting lines form 4 angles. We call the 2 angles that are next to each other and which form a straight line a "linear pair", or “supplementary angles”, and their sum is 180°.

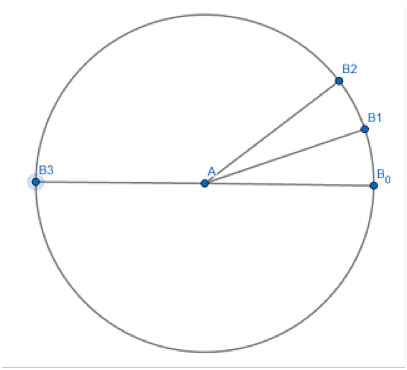
Why? Let’s take a line segment (AB), and start rotating it around one of its end-points:

The angle formed between the original segment (AB0) and the subsequent positions (AB1, AB2…) keeps growing. When we complete a full circle, the measure of the angle is 360°, because as we said above, that is what a full circle measures.

So when we rotate enough to make half a circle (to point B3), the measure is 180°. We know that when we rotate enough to make half a circle we will have a straight line because of symmetry – we could have rotated the line in either direction, and the half-way point would be the same.

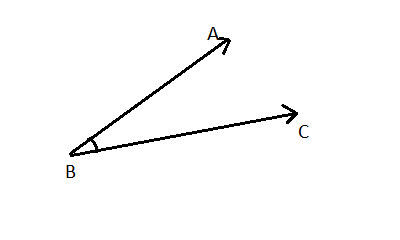
We describe angles using this notation: ∠1 or ∠α, and their measure in degrees as m∠1 or m∠α. We also commonly describe angles using the 3 points that define them, e.g: ∠ABC, where B is the vertex and BA and BC are the two rays that emanate from point B outward:

Angle Addition Postulate

The angle addition postulate states that if a point, P, lies inside an angle B then m∠ABP+m∠PBC=m∠ABC

In other words, the measure of the larger angle is the sum of the measures of the two interior angles that make up the larger one.

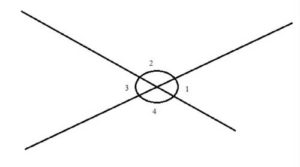
When two lines intersect and form 4 angles at the intersection, the two angles that are opposite each other are called “opposite angles” or “vertical angles” and these vertical angles are “congruent” – meaning they have the same shape and size. We say two angles are congruent if they have the same measure of their angle, in degrees. They are equal to each other. We note congruency using this symbol: ≅.

With the definitions and axioms presented so far, we can now start deriving our first theorem, using our first formal proof – proving that the opposite angles of two intersecting lines are congruent.

--
Now that we've explained the basic concept of intersecting lines and angles in geometry, let's scroll down to work on specific geometry problems relating to this topic.