In today's lesson, we'll see a detailed step by step proof of the vertical angles theorem, which says that opposite angles of two intersecting lines are congruent. Plus, learn how to solve similar problems on your own!
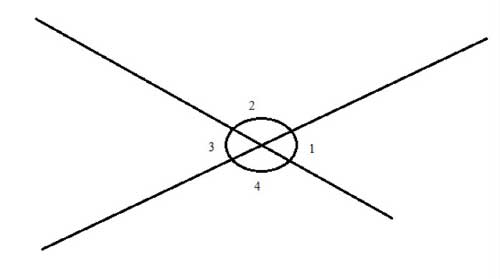
The Theorem
The Vertical Angles Theorem states that the opposite (vertical) angles of two intersecting lines are congruent.
The problem
Prove: ∠1 ≅∠3 and ∠2 ≅ ∠4
Proof
(1) m∠1 + m∠2 = 180° // straight line measures 180°
(2) m∠3 + m∠2 = 180° // straight line measures 180
(3) m∠1 + m∠2 = m∠3 + m∠2 // transitive property of equality, as both left-hand sides of the equation sum up to the same value (180° )
(4) m∠1 = m∠3 // subtraction property of equality (subtracted m∠2 from both sides)
(5) ∠1 ≅ ∠3 // definition of congruent angles
Similarly, for ∠2 ≅∠4:
(1) m∠3 + m∠2 = 180° // straight line measures 180°
(2) m∠3 + m∠4 = 180° // straight line measures 180°
(3) m∠3 + m∠2 = m∠3 + m∠4 // transitive property of equality, as both left hand sides of the equation sum up to the same value (180° )
(4) m∠2 = m∠4 // subtraction property of equality (subtracted m∠3 from both sides)
(5) ∠2 ≅ ∠4 // definition of congruent angle
And thus we have proven the theorem.
Quod erat demonstrandum
Often, you will see proofs end with the
Strategy: How to solve similar problems
Ok, great, I’ve shown you how to prove this
Well, in this case, it is quite simple. All we were given in the problem is a couple of intersecting lines. And the only definitions and proofs we have seen so far are that a line’s angle measure is 180
This problem has two sets of two supplementary angles which make up a straight line. So that’s the hint on how to proceed. Make use of the straight lines – both of them - and what we know about supplementary
