Chords

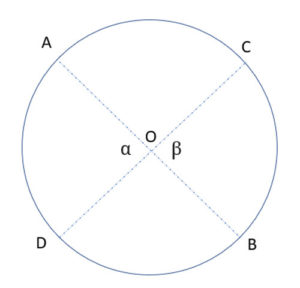
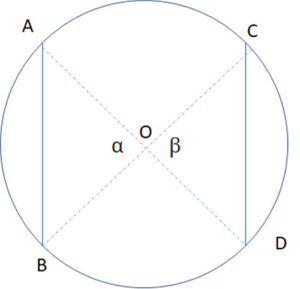
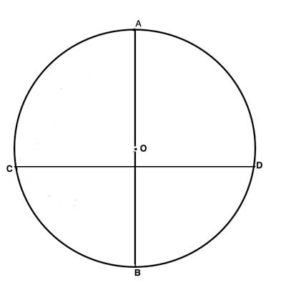
A chord is a straight line connecting two points on the circle.

The diameter is a special chord, which passed through the center of the circle, and its length is 2*r. It is the longest possible chord in the circle.

--
Now that we've explained the basic concept of chords in geometry, let's scroll down to work on specific geometry problems relating to this topic.