In today's lesson, we will prove that if a diameter bisects two chords in a circle, the two chords are parallel to each other. We can do this this three ways, relying on the properties of parallel and perpendicular lines.
Problem
In circle O, AB is a diameter that bisects two chords, CD and EF. Show that the chords are parallel to each other.
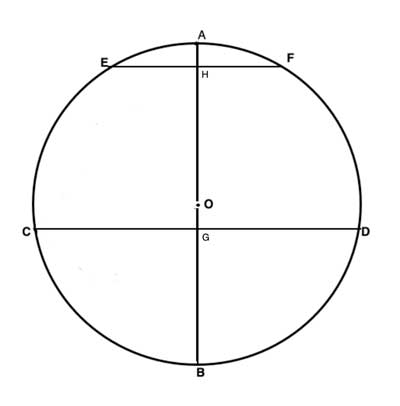
Strategy
To show two lines are parallel, we can use one of the several methods: either show congruent corresponding angles, congruent alternating interior angles, or the Perpendicular Transversal Theorem.
Since we have shown that the diameter that bisects a chord is perpendicular to that chord. any of these three methods will work, and all are as easy to show. We'll prove this using each of the three.
Proof
Here's how you prove that if a diameter bisects two chords, they are parallel to each other:
(1) AB bisects CD // Given
(2) AB⊥CD // A diameter that bisects a chord is perpendicular to that chord
(3) AB bisects EF // Given
(4) AB⊥EF // A diameter that bisects a chord is perpendicular to that chord
(5) ∠OGD ≅∠AHF=90° //(2), (4), definition of perpendicular lines
(6) EF||CD // congruent corresponding angles
Alternatively, we can repeat the first part of the proof, above, through step number (4), to show that AB is parallel to both CD and EF (AB⊥CD and AB⊥EF), and from there proceed as follows:
(5)' ∠OHF ≅∠OGC=90° //(2), (4), definition of perpendicular lines
(6)' EF||CD //Converse congruent alternating interior angles theorem
Finally, to prove this a third way, using the perpendicular transversal theorem, we again repeat the first part of the proof, above, through step number (4). This shows that AB is perpendicular to both CD and EF (AB⊥CD and AB⊥EF), and from there proceed as follows:
(5)'' EF||CD //(2),(4) Perpendicular Transversal Theorem.
