Chords that have an equal length are called congruent chords. An interesting property of such chords is that regardless of their position in the circle, they are all an equal distance from the circle's center. The distance is defined as the length of a perpendicular line from a point to a line.
Problem
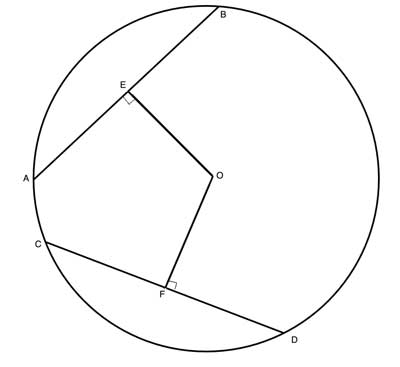
In circle O, the two chords AB and CD are congruent. Prove that they are equidistant from the point O.
Strategy
We can use triangle congruency to prove line segments are equal length. Since the distance is defined as the length of a perpendicular line from a point to a line, we are dealing with a perpendicular line to the chord, and we can rely on theorems about chords. Specifically, that a diameter or a radius that is perpendicular to a chord bisects that chord.
Since OE and OF are such lines that are perpendicular to the chords, they are also bisectors, and if we construct triangles using radii, as below, it is easy to show that they are congruent using the Hypotenuse-Leg postulate.

Proof
(1) AB=CD //Given, definition of congruent chords
(2) OE⊥AB //Given, definition of distance
(3) OF⊥CD //Given, definition of distance
(4) AE=EB=½AB //line from center of circle and perpendicular to a chord bisects the chord
(5) CF=FD=½CD //line from center of circle and perpendicular to a chord bisects the chord
(6) AE = CF //(1), (4), (5), halves of equal segments, transitive property of equality
(7) m∠OEA = m∠OFC=90° //(2), (3) definition of perpendicular lines
(8) OC=OA // Radii of a circle are all equal
(9) ΔOAE ≅ ΔOCF //Hypotenuse-Leg
(10) OE=OF //Corresponding sides in congruent triangles (CPCTC)
Converse Theorem
Having proven that congruent chords are equidistant from the center, let's use the exact same strategy to prove the converse, which is that chords that are equidistant form the circle's center are congruent. As above, we'll use the fact that distance is defined as the length of a perpendicular line from a point to a line, and so we have a perpendicular line to the chord. As above, a radius that is perpendicular to a chord bisects that chord, and it also bisects that chord.
With that, it is easy to prove the converse theorem:
(1) OE=OF //Given, chords are equidistant
(2) OE⊥AB //Given, definition of distance
(3) OF⊥CD //Given, definition of distance
(4) m∠OEA = m∠OFC=90° //(2), (3) definition of perpendicular lines
(5) OC=OA // Radii of a circle are all equal
(6) ΔOAE ≅ ΔOCF //(1), (4), (5) Hypotenuse-Leg
(7) AE=CF //Corresponding sides in congruent triangles (CPCTC)
(8) AE=EB=½AB //line from center of circle and perpendicular to a chord bisects the chord
(9) CF=FD=½CD //line from center of circle and perpendicular to a chord bisects the chord
(10) ½AB = ½CD //(7),(8), (9), transitive property of equality
(11) AB=CD //(10), multiply by two , multiplication property of equality
