What are congruent right triangles? We can use the properties of special triangles (like isosceles triangles or right triangles) to help us identify corresponding parts that are equal. Let's look at an example:
Problem
Two right triangles, ΔABC and ΔDEF have an equal hypotenuse and equal leg. Prove that the triangles are congruent.
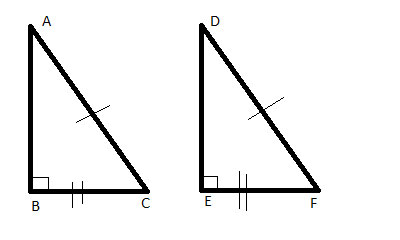
Strategy
Looking at the two triangles, we see we have two equal sides - the legs AB and DE, and the hypotenuses AC and DF - this was given in the problem statement.
We also have one pair of congruent angles- the right angles ∠ABC and ∠DEF, as both triangles are right triangles.
Unfortunately, we can't use the Side-Angle-Side postulate, because the congruent angle is not between the two sides.
It is tempting to try and find another pair of angles, but we simply don't know anything about the other two angles. BUT we do know something else about right triangles, which is the relationship between their legs and the hypotenuse- the Pythagorean theorem: a² + b² = c².
Here we already have 2 of the sides being equal, so we can algebraically show that the third side must also be equal and prove that the triangles are congruent using the Side-Side-Side postulate.
Proof
(1) AB = DE //given
(2) AC = DF //given
(3) m∠ABC = m∠DEF=90° // Definition of right triangle
(4) AB² + BC² = AC² //Pythagorean theorem
(5) DE² + EF² = DF² // Pythagorean theorem
(6) AB² + EF² = AC² //substitution using (1), (2) & (5)
(7) BC = EF //(4) & (6)
(8) ΔABC ≅ΔDEF // Side-Side-Side postulate
You will sometimes see this referred to as yet another method for showing triangle congruency, applicable only to right triangles, called 'Hypotenuse-Leg' (or HL, for short) - if two right triangles have the same hypotenuse and one leg, they are congruent.
