What Are Parallel Lines in Geometry?

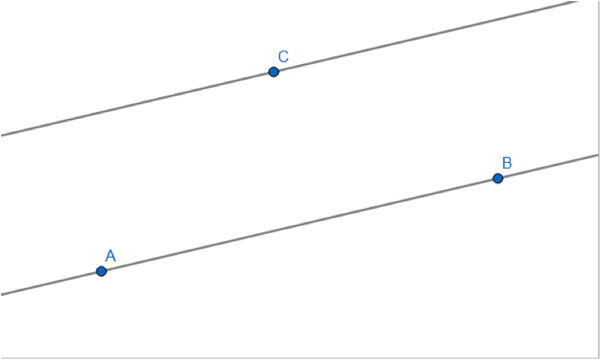
As we wrote earlier, an axiom of Euclidean geometry is that for every straight line and every point not on that line, there is one straight line that passes through that point, and never intersects the first line. Such lines are called Parallel lines.

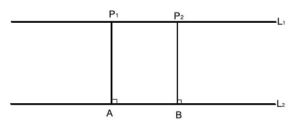
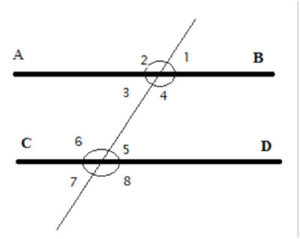
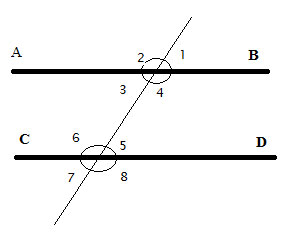
Parallel lines are always the same distance from each other. We use this notation - ||- to describe two parallel line segments, for example: AB||CD

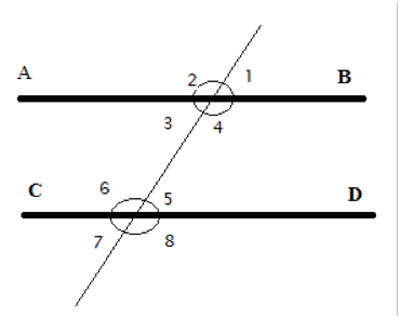
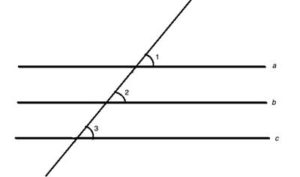
When a third line intersects two parallel lines, as above, it creates 4 angles with each one of the lines. The angles in the same position, for example, above the line and to the right, like 1 and 5, above, are called corresponding angles. The two pairs of angles that are on the “inside” of the parallel lines (4 & 5, and 3 & 6) are called “interior angles”.
The two pairs of angles that are on the “outside ” the parallel lines (1 & 8, and 2 & 7) are called “exterior angles”.

The line crossing and intersecting the parallel lines is called the transversal line. Another way of stating the parallel line axiom (”for every line and every point not on that line, there is one straight line that passes through that point, and never intersects the first line“) is that a transversal line intersects parallel lines creating corresponding angles that are congruent. This has no proof- it is another way of stating the axiom.

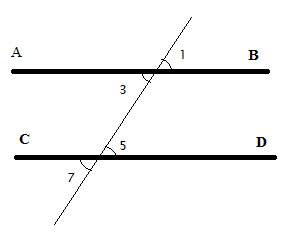
We will now prove several theorems about the angles formed by the intersection of the transversal line and the two parallel lines. You can click on each one of the proofs below. Once you review them all you will find that we have shown that when two parallel lines are intersected by a transversal line, the following angles are all the same:

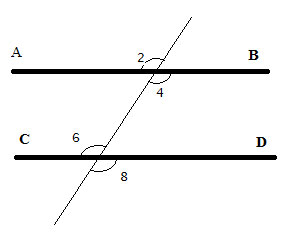
And also that the following angles are all the same:

--
Now that we've explained the basic concept of parallel lines in geometry, let's scroll down to work on specific geometry problems relating to this topic.