In today's lesson, we will show that two lines parallel to a third line are parallel to each other.
In geometry, parallel lines are lines that do not meet. They do not intersect or touch each other at any point. This definition first appeared very early, in Book I of Euclid's Elements.
One way to show that two lines are parallel to each other is to find two corresponding angles created by a transversal line that are congruent, as we have proven in this lesson.
We can use this theorem to come up with another way to show two lines are parallel- if they are both parallel to a third line.
Problem
If line a is parallel to b, and line c is also parallel to b, show that line a is parallel to c.
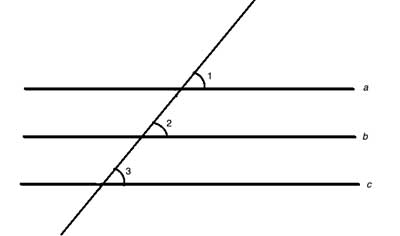
Strategy
We can show lines are parallel by finding a pair of corresponding angles that are congruent. Parallel lines form congruent angles when intersected by a third line. So let's draw a transversal line that intersects all three lines.
Line a is parallel to b, so ∠1 ≅ ∠2 which means that m∠1 = m∠2. Similarly, c is also parallel to b, so ∠2 ≅ ∠3 which means that m∠2 = m∠3. Using the transitive property of equality, m∠1 = m∠3, and so ∠1 ≅ ∠3.
And now, by using the converse of the corresponding angles theorem, line a is parallel to line c.
Proof
This is how you show that two lines parallel to a third are parallel to each other:
(1) a||b //Given
(2) ∠1 ≅ ∠2 //corresponding angles formed by third line intersecting parallel lines are equal
(3) m∠1 = m∠2 //Definition of congruent angles
(4) b||c //Given
(5) ∠2 ≅ ∠3 //corresponding angles formed by third line intersecting parallel lines are equal
(6) m∠2 = m∠3 //Definition of congruent angles
(7) m∠1 = m∠3 //(3), (6), transitive property of equality
(8) ∠1 ≅ ∠3 //(7), definition of congruent angles
(9) a||c // Converse of the Corresponding Angles Theorem