If you connect the midpoints of the sides of any quadrilateral, the resulting quadrilateral is always a parallelogram.
Surprisingly, this is true whether it is a special kind of quadrilateral like a parallelogram or kite or trapezoid, or just any arbitrary simple convex quadrilateral with no parallel or equal sides.
Problem
In a quadrilateral ABCD, the points P, Q, R and S are the midpoints of sides AB, BC, CD and DA, respectively. Prove the PQRS is a parallelogram.
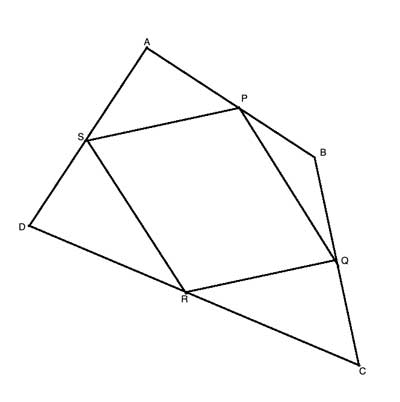
Strategy
The fact that we are told that P, Q, R and S are the midpoints should remind us of the Triangle Midsegment Theorem - the midsegment is parallel to the third side, and its length is equal to half the length of the third side.
We have no triangles here, so let's construct them, so the midpoints of the quadrilateral become midpoints of triangles, by drawing the diagonal AC:
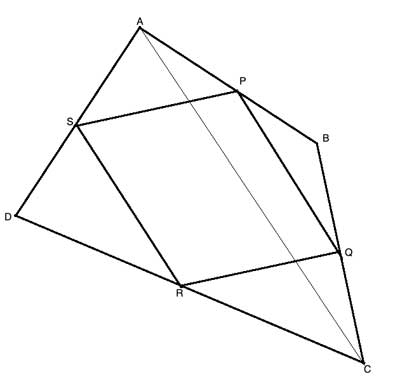
We now have two triangles, ΔBAC and ΔDAC, where PQ and SR are midsegments. So, using the Triangle Midsegment Theorem we find that PQ||AC and PQ = ½AC, and also that SR||AC and SR = ½AC.
Since PQ and SR are both parallel to a third line (AC) they are parallel to each other, and we have a quadrilateral (PQRS) with two opposite sides that are parallel and equal, so it is a parallelogram.
We could have also done this by drawing the second diagonal DB, and used the two triangles ΔADB and ΔCDB instead.
Proof
This is how you show that connecting the midpoints of quadrilateral creates a parallelogram:
(1) AP=PB //Given
(2) BQ=QC //Given
(3) PQ||AC //(1), (2), Triangle midsegment theorem
(4) PQ = ½AC //(1), (2), Triangle midsegment theorem
(5) AS=SD //Given
(6) CR=RD //Given
(7) SR||AC //(5), (6), Triangle midsegment theorem
(8) SR = ½AC //(5), (6), Triangle midsegment theorem
(9) SR=PQ //(4), (8), Transitive property of equality
(10) SR||PQ //(3), (7), two lines parallel to a third are parallel to each other
(11) PQRS is a Parallelogram //Quadrilateral with two opposite sides that are parallel & equal
