Arcs, Angles, and Sectors

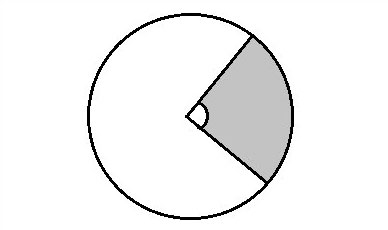
An arc is a curved line segment that makes up part of the circle. The end-points of the arc on the circle's circumference defines two arcs, one in each direction.

If the two points lie at the ends of a diameter, the two arcs will be the same size. Otherwise, there will be one large arc called the major arc, and the smaller one the minor arc.

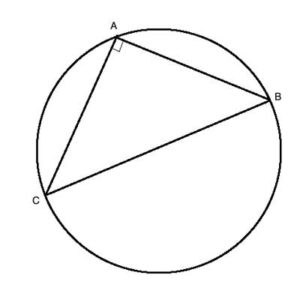
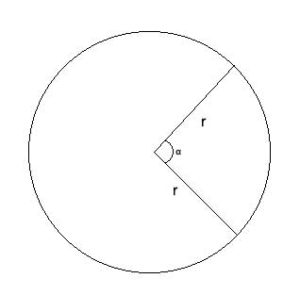
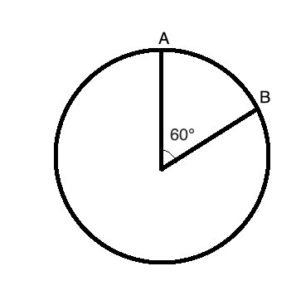
If we draw lines from the center of the circle to the end-points of the arc (these lines are both radii), we will define an angle called a Central Angle. If we draw chords from a point on the circle to each of the endpoints of the arc, we will define an angle called an Inscribed angle.

The Inscribed Angle's measure is half that of the central angle of the same arc, as we will prove in the problem set.

The area between an arc and the two radii lines from the center of the circle to the arc's end-points is called a sector.
--
Now that we've explained the basic concept of arcs, angles and sectors in geometry, let's scroll down to work on specific geometry problems relating to this topic.