In today's lesson, we will show that the Inscribed angle's measure is half that of the central angle of the same arc.
If we draw lines from the center of the circle to the end-points of an arc on the perimeter of a circle, (these lines are both radii), we will define an angle called a Central Angle.
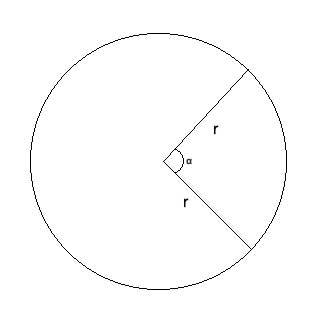
If we draw chords from a point on the circle perimeter to each of the endpoints of an arc, we will define an angle called an Inscribed Angle.
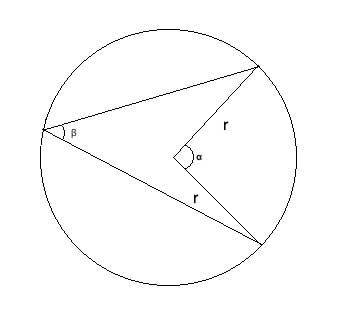
The inscribed angle's measure is half that of the central angle of the same arc, as we will now prove. This will be a long proof, as it needs to address several different cases - so fasten your seat belt!
Problem
Show that an inscribed angle's measure is half of that of a central angle that subtends, or forms, the same arc.
Strategy
When proving the Inscribed Angle Theorem, we will need to consider 3 separate cases:
The first is when one of the chords is the diameter.
The second case is where the diameter is in the middle of the inscribed angle.
And the third case is when the diameter is outside the inscribed angle.
These three cases cover all the possibilities (the diameter is either inside the inscribed angle, outside the inscribed angle, or is one of the chords forming the inscribed angle), so if we prove the Inscribed Angle Theorem for each one of the cases, we will have the complete proof.
First case: One of the chords forming the inscribed angle is the diameter
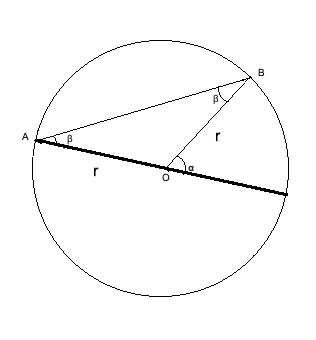
In this case, OA and OB are both radii, and are thus equal to each other. This means that the triangle ΔOAB is isosceles, and we know that the base angles of an isosceles triangle are congruent, so ∠OAB ≅∠OBA = β.
But from the exterior angle theorem, we know that α, as the exterior angle to triangle ΔOAB, is equal to the sum of the two remote angles, ∠OAB and∠OBA so:
m∠α = m∠OAB +m∠OBA=m∠β+m∠β= 2*m∠β and we have proven that for this case, where one of the chords of the inscribed angle β is the diameter, the central angle is twice the inscribed angle α.
Second case: the diameter is in the middle of the inscribed angle

Having just proven the first case, let's try to use what we just proved, and draw the diameter:

And now we can just treat this case as two instances of the first case, one where the inscribed angle β1 has a chord which is the diameter, and the other where the inscribed angle β2 has a chord which is the diameter, and apply what we have just proved for the case where the chord is the diameter:
So, from the first case, m∠α1=m∠β1+m∠β1= 2*m∠β1, and
m∠α2=m∠β2+m∠β2= 2*m∠β2.
Adding these two equations we get
m∠α1+m∠α2= 2*m∠β1+2*m∠β2
and from the angle addition postulate, we know m∠α1+m∠α2 = m∠α and m∠β1+m∠β2=m∠β, so
m∠α= 2*m∠β, and we have proven the second case, as well.
Third and final case: the diameter lies outside the inscribed angle
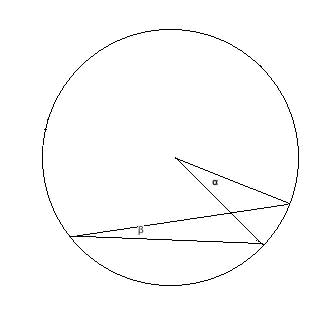
Drawing the diameter really helped us in the second case, because we could then easily leverage what we proved in the first case. So let's see if the same trick works again, and draw the diameter from the apex of the inscribed angle:
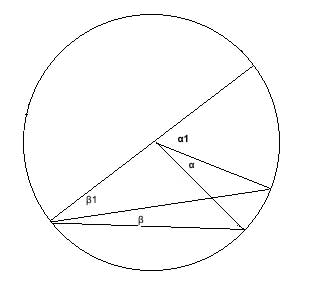
We can now again treat this as a case of two inscribed angles having a diameter as one of the chords.
The first inscribed angle is β1, and the second inscribed angle is (β+β1). α1 is a central angle that subtends the same arc as β1, so it is equal to 2*β1 (as proven for the first case), and the angle (α1+α) is a central angle that subtends the same arc as (β+β1) so it is equal to 2*(β+β1) (again, as proven for the first case).
So we have:
m∠α1= 2*m∠β1
m∠α1+m∠α= 2*m∠(β1+β)
And from the angle addition postulate, we get
m∠α1+m∠α= 2*m∠β1+2*m∠β
Subtract the first equation from this last one, and we get
m∠α= 2*m∠β and we are done, having proven all three cases.
An interesting result of the Inscribed Angle Theorem is that the only thing that matters is the arc on the perimeter. Any two inscribed angles that subtend that arc are equal.
