Problem
Prove that the exterior angle at a vertex of a triangle is equal to the sum of the remote interior angles.
We know that the sum of the angles in a triangle is 180°. So now it is simple to prove a corollary theorem.
Here we will prove that the measure of an exterior angle at a vertex of a triangle is equal to the sum of the measures of the interior angles at the other two vertices of the triangle (called the remote interior angles).
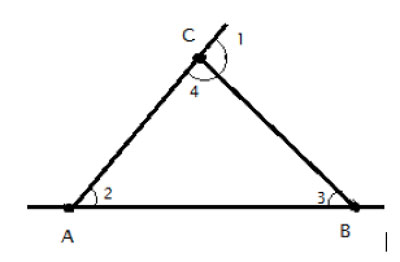
Strategy
Here we combine our knowledge of two sets of angles that sum up to 180°. A linear pair of angles (that make up a straight line), and the interior angles of a triangle.
Since both sets add up to the same total, and one angle is common to both (∠4), the others must be equal.
Proof
(1) m∠1 + m∠4 = 180° // straight line measures 180°
(2) m∠2 + m∠3+ m∠4 = 180° //sum of the interior angles in a triangle
(3) m∠1 + m∠4 = m∠2 + m∠3+ m∠4 //(1), (2), transitive property of equality, both equal 180°
(4) m∠1 = m∠2 + m∠3 // subtraction property of equality (subtracted m∠4 from both sides)
Exterior Angle Inequality Theorem
Now that we have proven that the exterior angle is equal to the sum of the remote interior angles, it is trivial to prove the corollary Exterior Angle Inequality Theorem, which states that the exterior angle is larger than either of the remote angles. Since it is equal to the sum of the angles, and the measure of an angle in a triangle is always a positive number, it must be larger than either one. The formal two-column proof is:
| (1) m∠1 = m∠2 + m∠3 | //Exterior angle theorem, as above |
| (2) m∠2 >0 | //Angles of a triangle are always positive |
| (3) m∠1 > m∠3 | //1,2,Comparison property of inequality |
| (4) m∠3 >0 | //Angles of a triangle are always positive |
| (5) m∠1 > m∠2 | //1,4,Comparison property of inequality |
