The Sum of Interior Angles in a Simple Convex Quadrangle

In today's lesson, we will prove that the sum of interior angles in a simple convex quadrangle is always 360° by showing that this quadrangle is composed of two triangles.

Problem

Show that the sum of interior angles in a simple convex quadrangle is always 360°.

Strategy

Let’s think about the strategy to answer this geometry problem. 360 is a familiar number - it is the measure of angles in a circle, but there are no circles here, so let’s rule that out.

360 is also 2x180, and that is also a familiar number. It is the sum of the angles in a triangle.

So, if we can show that this quadrangle is composed of two triangles, we will have the proof- and that’s all we need.

Proof

In any simple convex polygon, a line connecting 2 points on the perimeter of the polygon is entirely within the polygon, per the definition of convex polygons.

So, let’s draw a line connecting two opposite corners of the quadrangle (such a line is a called a ‘diagonal’) – say from C to A:

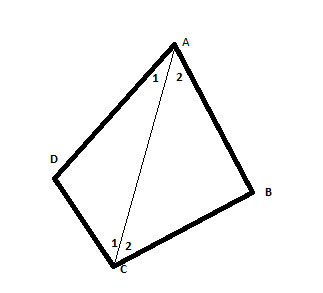
(1)    m∠A₁ + m∠D+ m∠C₁ = 180°                        //sum of the interior angles in triangle ΔADC

(2)    m∠A₂ + m∠B+ m∠C₂ = 180°                         //sum of the interior angles in triangle ΔABC

(3)    m∠A₁ + m∠D+ m∠C₁+m∠A₂ + m∠B+ m∠C₂ = 360°   //add both equations

(4)    m∠A₁ + m∠A₂ +m∠D+ m∠C₁+ m∠C₂ + m∠B= 360°   //re-arrange terms

(5)    m∠A₁ + m∠A_{2 =} m∠A                                      // angle addition postulate

(6)    m∠C₁ + m∠C_{2 =} m∠C                                       // angle addition postulate

(7)    m∠A+m∠D+ m∠C + m∠B= 360°   ∎         //substitution property of equality