In today's lesson, we'll ask what are polygons in geometry. We'll also discuss types of polygons - regular, simple, complex, and more.
Definition
A polygon is a two-dimensional (flat) shape. We create polygons by connecting a number of straight lines to form a closed shape. Circles and ellipses are not polygons, because their edges are not straight lines.
We name polygons according to the number of sides they have. That is, the number of straight-line segments that are used in drawing the shape. A polygon with three sides is a triangle. A polygon with four sides is a quadrangle, and so on.
Types of polygons
Regular polygons
If all the sides of a polygon are of equal length, and all its angles have the same measure, we call it ‘regular’.
Simple polygons
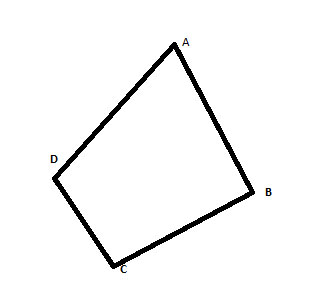
Simple polygons have sides that do not intersect or cross each other:
Complex polygons
Complex polygons have sides that intersect, for example:
Convex polygons
Convex polygons are simple polygons where all the interior angles measure less than 180°. The polygons vertices point "outward" from its center.
Concave polygons
In Concave polygons, there is at least one interior angle which measure more than 180°:
Our focus: simple convex polygons
We will only concern ourselves with simple convex polygons. It is rare to see high school geometry problems that involve concave polygons, and even rarer to see ones involving self-intersecting polygons.
In addition, even those problems that do involve such polygons typically have answers that involve treating those complex polygons as a number of simple polygons side by side. For example, look at the complex polygon illustrated above. In most cases, we could simply treat it as if it was a triangle connected to a quadrilateral at one point of intersection.