In today's lesson, we'll discuss the concepts of lines and angles in geometry, including line segments, line axioms, and how two intersecting lines form an angle.
What is a line?
A line is an abstract concept. It has no width, only length, and that length is infinite in both directions. One of the formal definitions of a line is that it is the collection of all points that are the same distance from two other points on a plane:
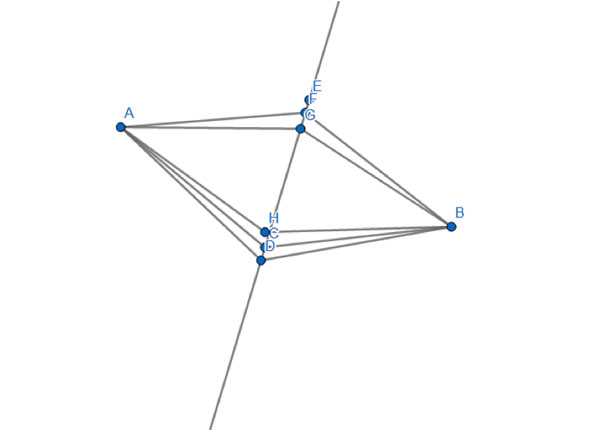
Each one of the points C, D, E, F, G and H is the same distance from A and B. If we drew all the possible points that are like this, we’d have the line drawn above.
Line segments
A straight line extends infinitely in both directions. But we often deal with a specific part of the line, defined by two points on the line. Such parts are called line segments, and are defined by the two points. For example, in drawing above we have a line segment between points G and H, called GH, another segment between D and (DG) and so on.
Line axioms
In Euclidean geometry (which is the kind of geometry we use here), it is an axiom that you can draw a line between any two points. An axiom is something taken as a basic rule which is self-evident, it does not have a proof.
Another axiom is that for every straight line and every point not on that line, there is one straight line that passes through that point, and never intersects the first line. Such lines are called Parallel lines, which we will deal with in a subsequent section.
Angles
When 2 lines or line segments intersect, they form angles:

We measure angles in units called degrees, and marked with a °, where a full circle is 360°. Why 360? It is just a very convenient number, because it is divisible by many other numbers – 2,3,4,5,6,9, 10, 12….
