In today's lesson, we'll prove the Linear Pair Perpendicular Theorem: This theorem states that if two straight lines intersect at a point, and the linear pair of angles they form have an equal measure, then the two lines are perpendicular to each other.
Problem
If two straight lines intersect at a point and form a linear pair of equal angles, they are perpendicular.
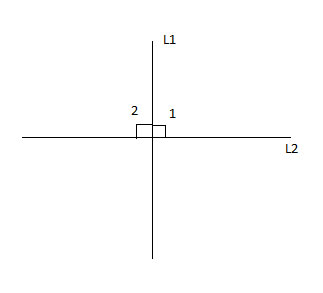
in other words, given m∠1 = m∠2, prove that the lines L1 and L2 are perpendicular.
Strategy
To prove that lines are perpendicular, we need to find an angle that measures 90°. In the problem statement, we are given the fact that we have a linear pair of angles, and that they are equal. The hint here is "linear pair" - we know those measure 180°, and 180° is twice 90°.
Proof
(1) m∠1 = m∠2
(2) m∠1 + m∠2 = 180° // straight line measures 180°
(3) m∠1 + m∠1 = 180° // using (2) and performing algebraic substitution, replacing m∠2 with the equivalent m∠1
(4) 2 • m∠1 = 180° // Simplify, using multiplication
(5) m∠1 = 180°/2= 90° //algebraically solve for m∠1
(6) L1 ⊥ L2 //per the definition of perpendicular lines.