Pythagorean Theorem

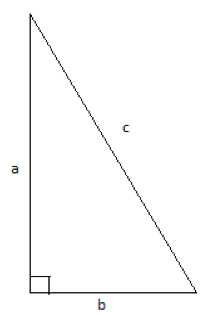
The Pythagorean theorem, named after the Greek mathematician Pythagoras who first proved it, is fundamental to many geometry problems, and later on, for trigonometry.

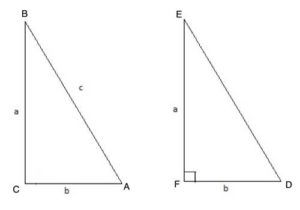
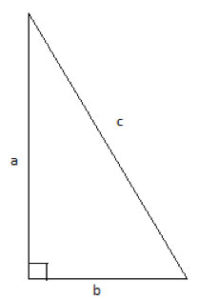
The theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the two legs:

c^{2 =} a²+b²

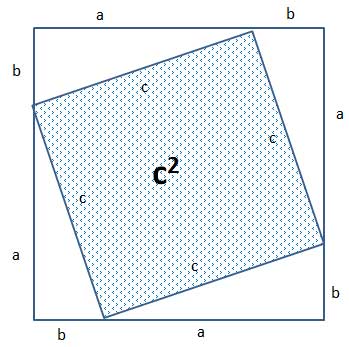
Pythagoras used proof by rearrangement to show that the relationship holds. He started out by creating 4 copies of the right triangle, and arranging them in a square, like so:

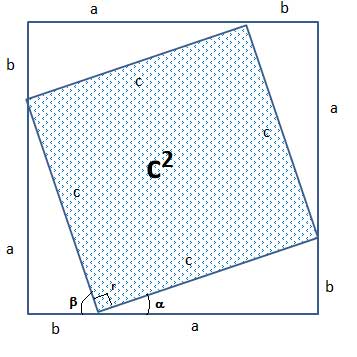
Since all the triangles are the same (they are copies of each other), it is easy to see that inside the outer square formed by the triangles' legs, there is an inner square formed by the hypotenuses.

We know it is a square because it is a quadrangle, all its sides are equal since they are copies of the same hypotenuse, and the interior angle is 90°.

The interior angle, r, is 90° because the three angles α, β and r form a linear angle whose measure is 180°, while α+β =90° because they are the two non-right angles in the right triangle.

The edges of that square all measure c in length, so its area is c*c, or c squared.

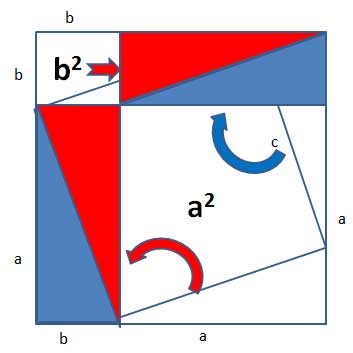
We can now rearrange those triangles, staying within the exterior square: rotate the bottom right triangle 90° counter-clockwise, so that it is vertical. Rotate the top right triangle 90° clockwise so that it is horizontal. And push the top left triangle to the right, like this:

Since the outer square has not changed, and the triangles have not changed size or shape, only position, the new white area should be the same area as before,  c^2.

But this new white area is made up of 2 squares- the top left measuring b * b= b² and the bottom right one measuring a * a= a²

So the previous white area, c² , must be equal to this new white area, a²+b², and the theorem is proven.

--
Now that we've explained the basic concept of the Pythagorean theorem in geometry, let's scroll down to work on specific geometry problems relating to this topic.