Converse of the Pythagorean Theorem

One of the most useful theorems in Euclidean geometry, which we have used often in other proofs is the Pythagorean Theorem.

The Pythagorean Theorem states that in a right triangle, the following relationship holds between the two legs (a, b) and the hypotenuse (c) :

c^{2 =} a²+b²

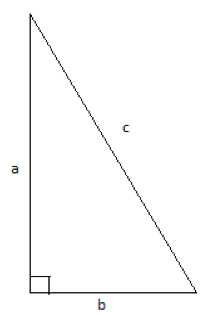
We've proven this theorem two ways, one using geometric shifting and rearrangement, the way Pythagoras proved it. Subsequently, after covering the concept of similarity, we proved it using similar triangles.

But what about the converse case? If we know that in a triangle the three sides are related so that c^{2 =} a²+b², is it necessarily a right triangle? It turns out that the answer is yes, as we will now prove, using the converse of the Pythagorean Theorem.

Problem

In triangle ΔABC with sides AB, BC and AC, |BC|²+|AC|²=|AB|². Prove that the triangle is a right triangle

Strategy

Intuitively, it seems obvious that the converse is true, and that's usually a hint to try and use proof by contradiction. We'll assume the theorem is false.

That is, that the triangle is not a right triangle, and try to arrive at a logical contradiction. That means the assumption is false, and as a result, the triangle must be a right triangle.

As a first step, let's construct a right triangle ΔDEF, such that |EF|=|BC|, |DF|=|AC|, and m∠EFD=90°.

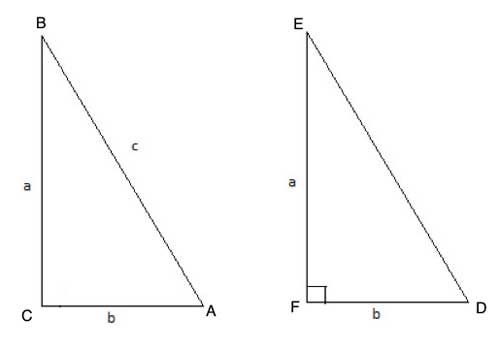
Since ΔDEF is a right triangle, by the Pythagorean theorem, |EF|²+|DF|²=|ED|².

As given the problem statement, |BC|²+|AC|²=|AB|². We constructed ΔDEF, such that |EF|=|BC|, |DF|=|AC|, so substituting |EF| for |BC| and |DF| for |AC|, we get |EF|²+|DF|²=|AB|²=|ED|². Since all these quantities are lengths of sides, they are positive, and so we can conclude that |AB|=|ED|.

But if all the sides are equal, then ΔDEF and ΔABC are congruent, by the Side-Side-Side postulate. And if they are congruent, ∠EFD ≅ ∠BCA, and because we constructed ∠EFD such that m∠EFD=90° it follows that m∠BCA=90°.

We have contradicted our assumption that ΔABC is not a right triangle. The assumption is thus false, and ΔABC is a right triangle. And so we have proved the converse of the Pythagorean Theorem.

Proof

(1) Assume ΔABC is not a right triangle //Assumption
(2) |EF|=|BC| //Construction
(3) |DF|=|AC| //Construction
(4) m∠EFD=90°  //Construction
(5) |EF|²+|DF|²=|ED|² //(4), Pythagorean theorem
(6) |BC|²+|AC|²=|AB|² //Given
(7) |EF|²+|DF|²=|AB|² //(2),(3),(6), substitution
(8) |ED|²=|AB|² //(5),(7), transitive property of equality
(9) |ED|=|AB| //(8), quantities are positive (lengths of sides)
(10) ΔDEF ≅ ΔABC //(2),(3),(9), Side-Side-Side postulate
(11) ∠EFD ≅ ∠BCA //Corresponding angles in congruent triangles
(12) m∠EFD=m∠BCA=90°  //(4), defintion of congruent angles
(13) m∠BCA=90°  contradicts (1)