Rhombus

A parallelogram in which all the edges are of equal length is called a rhombus, or a diamond.

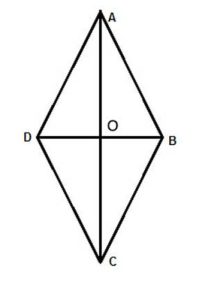
In addition to the general properties of parallelograms, in a rhombus, the diagonals bisect the angles, and the diagonals are perpendicular to each other.

We will show these properties using triangle congruence.

--
Now that we've explained the basic concept of rhombus in geometry, let's scroll down to work on specific geometry problems relating to this topic.