What is the shape of the quadrilateral formed by joining the midpoints of a rhombus? In an earlier post, we saw that the quadrilateral formed by joining midpoints of any quadrilateral is a parallelogram. What if instead of a random quadrilateral we join the midpoints of a special quadrilateral, like a rhombus? Will we get a “special” parallelogram? The answer is yes!
In this post, we’ll see that the quadrilateral formed by joining the midpoints of a rhombus is a rectangle.
Problem
Strategy
To save work, we will rely on what we have already proven. A rhombus is a quadrilateral, so joining its midpoints creates a parallelogram. To prove this parallelogram Is a rectangle, we need to show that one of its interior angles is a right angle.
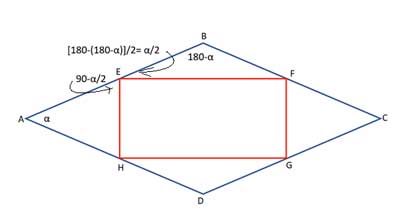
To show this, we will use the properties of a rhombus. In a rhombus, all the sides are equal. It follows that all the “half sides” formed by the midpoints are equal. This means that the triangles formed between the rhombus and the red parallelogram are all isosceles triangles. And in isosceles triangles, the base angles are equal.
Since a rhombus is a kind of a parallelogram, the sum of two of its adjacent interior angles is 180°. Now, we perform a little bit of angle math. We’ll use the fact that the sum of the consecutive interior angles ∠BAD and ∠ABC is 180°, the sum of the angles in triangle △EAH is 180°, as is the sum of the angles in triangle △BEF. Finally, the sum of the angles forming the straight-line BEA is also 180°, and the result is that angle ∠FEH measures 90°.
Proof
(1) ABCD is a rhombus //Given
(2) AB=AD //(1), Definition of a rhombus
(3) AE=AB/2 //Given, E is the midpoint of AB
(4) AH=AD/2 //Given, H is the midpoint of AD
(5) AE=AH //(2),(3),(4), substitutions
(6) m∠AEH = m∠AHE //(5), Base angle theorem
(7) BA=BC //(1), Definition of a rhombus
(8) BE=BA/2 //Given, E is the midpoint of BA
(9) BF=BC/2 //Given, F is the midpoint of BC
(10) BE=BF //(7),(8),(9) , substitutions
(11) m∠BEF = m∠BFE //(10), Base angle theorem
(12) m∠BAD+ m∠ABC = 180° //(1), adjacent interior angles of a parallelogram are supplementary
Now, let's refer to ∠BAD as 'α', then:
(13) m∠AEH= 90° -α/2 //(6), sum of angles in a triangle
(14) m∠BEF= [180° - (180° - α)]/2= α/2 //(12),(11), sum of angles in a triangle
(15) m∠AEH+m∠BEF+m∠FEH=180° //Straight line measures 180°
(16) 90° - α/2+ α/2+m∠FEH=180° //(13),(14),(15), substitutions
(17) m∠FEH=90° //rearrange and simplify (16)
(18) EFGH is a parallelogram //Connecting midpoints of a quadrilateral
(19) EFGH is a rectangle //(17), (18) , definition of rectangle
Another Strategy
All that angle math is somewhat complex, and might not be obvious. So let's try proving the same thing another way. We will still rely on what we have already proven: a rhombus is a quadrilateral, so joining its midpoints creates a parallelogram.
But as we are dealing with midpoints, it might be more intuitive to try and use the theorems we have proven about midpoints in a triangle - like the fact that the midsegment connecting two midpoints is parallel to the third side.
And we will also use the properties of a rhombus - in this case, that the sides are all equal, and that the diagonals of a rhombus bisect the angles.
Let's draw one of the diagonals, AC.
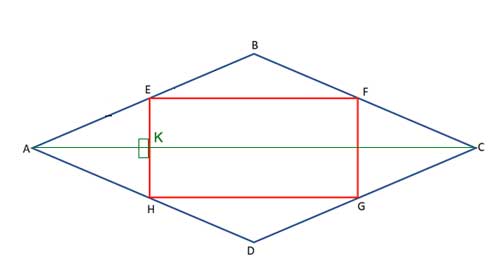
Armed with the above knowledge, we know that AD=AB as sides in a rhombus, and so their halves, AE and AH are also equal. AC is a diagonal in a rhombus, so it bisects the angle ∠BAD. It is now easy to show that triangles △EAK and △HAK are congruent, using the side-angle-side postulate. Then ∠AKE≅∠AKH as corresponding angles in congruent triangles, and since they form a linear pair, they must both be right angles. As a result, ∠EKC is also a right angle.
Alternatively, we could have also relied on what we have just proven above- that △EAH is isosceles, and that in an isosceles triangle the angle bisector of the apex is perpendicular to the base. The result is the same- ∠EKC is a right angle.
Now, using the triangle midsegment theorem, EF, the midsegment, is parallel to AC, so m∠KEF+m∠EKC=180°, and that means m∠KEF=90°, which is what we needed to prove.
Proof (2)
(1) ABCD is a rhombus //Given
(2) AB=AD //(1), Definition of a rhombus
(3) AE=AB/2 //Given, E is the midpoint of AB
(4) AH=AD/2 //Given, H is the midpoint of AD
(5) AE=AH //(2),(3),(4), substitutions
(6) ∠EAK ≅∠HAK //(1), Diagonal of rhombus bisects the angle
(7) AK=AK //Common side, reflexive property of equality
(8) △EAK ≅△HAK //(5),(6),(7), Side-Angle-Side Postulate
(9) ∠AKE≅∠AKH //(8), Corresponding angles of congruent triangles
(10) m∠AKE= m∠AKH= 90° //(9) , linear pair perpendicular theorem
(11) m∠EKC= 90° //(10), linear pair with ∠AKE
(12) AE=EB //Given, E is the midpoint
(13) BF=FC //Given, F is the midpoint
(14) EF||AC //Triangel midsegment theorem
(15) m∠KEF+m∠EKC=180° //(14), adjacent interior angles of a parallelogram are supplementary
(16) m∠KEF+ 90°=180° //(11), substitution
(17) m∠KEF=90°
(18) EFGH is a parallelogram //Connecting midpoints of a quadrilateral
(19) EFGH is a rectangle //(17), (18), definition of rectangle
A fun little fact is that while we've just shown that the quadrilateral formed by joining midpoints of rhombus is a rectangle, the quadrilateral formed by joining midpoints of rectangle is a rhombus!
