Proving The Base Angles Theorem

We will prove most of the properties of special triangles like isosceles triangles using triangle congruency because it is a useful tool for showing that two things - two angles or two sides - are congruent if they are corresponding elements of congruent triangles.

So, here's what we'd like to prove: in an isosceles triangle, not only are the sides equal, but the base angles equal as well.

Problem

Prove that in isosceles triangle ΔABC, the base angles ∠ACB and ∠ABC are congruent.

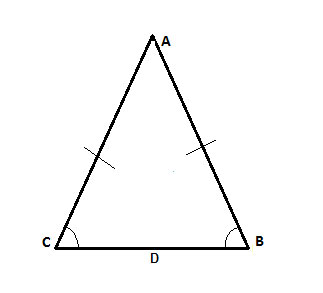
Strategy

So how do we go about proving the base angles theorem?

This problem is typical of the kind of geometry problems that use triangle congruency as the tool for proving properties of polygons.

Triangle congruency is a useful tool for the job. If we can place the two things that we want to prove are the same in corresponding places of two triangles, and then we show that the triangles are congruent, then we have shown that the corresponding elements are congruent.

This is the basic strategy we will try to use in any geometry problem that requires proving that two elements (angles, sides) are equal.

Ok, but here we only have one triangle, and to use triangle congruency we need two triangles. So let's think about a useful way to create two triangles here. We know that ΔABC is isosceles, which means that AB=AC, so it will be good if we place these two sides in different triangles, and already have one congruent side.

Then, we also want ∠ACB and ∠ABC to be in different triangles, to prove their congruency.

Putting these two things together, it would make sense to create the following two triangles, by connecting A with the mid-point of the base, CB:

Base angles theorem with corresponding parts marked

And now we have two triangles, ΔABD and ΔACD, where the angles we want to prove are congruent are in corresponding places. If we show that the triangles are congruent, we are done with this geometry proof.

So how do we show that the triangles are congruent? Easy! Using the Side-Side-Side postulate:

Proof

(1) ΔABC is isosceles //Given

(2) AB=AC // Definition of an isosceles triangle

(3) BD = DC // We constructed D as the midpoint of the base CB

(4) AD = AD // Common side to both triangles

(5) △ABD≅△ACD // SSS postulate

(6) ∠ACB ≅ ∠ABC // Corresponding angles in congruent triangles (CPCTC)

Another way to prove this theorem

I think the only "tricky" part of the above proof was the intuition required to draw the line connecting A with the middle of the base. So what if you didn't have that intuition? Well, luckily, we can prove this in another way.

We will still use triangle congruency. But this time, suppose you didn't think of drawing a line to the middle of the base. Instead, what if we draw a line that bisects the apex (or top) angle:

Again we have two triangles, ΔABD and ΔACD, where the angles we want to prove are congruent are in corresponding places. And we'll show the triangles are congruent using the Side-Angle-Side postulate: