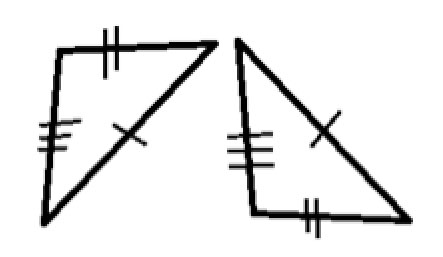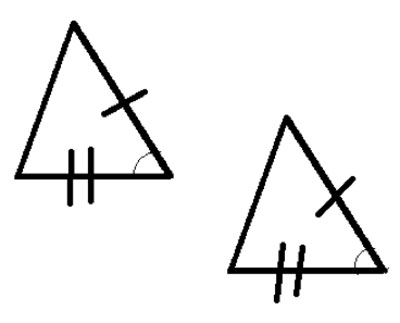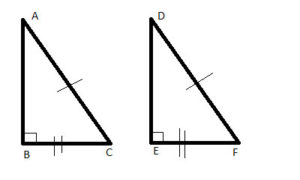Geometry Help
menu icon
search icon
×

Congruent Triangles

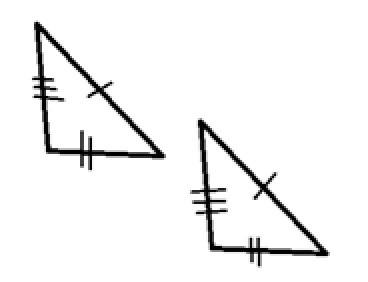
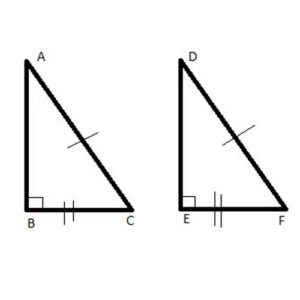
Two triangles that have the same three sides (same length) and the same angles (same angle measures) are said to be “congruent”, or the same:

Congruent triangles

We mark the corresponding equal sides with one line, two lines and three lines, as above.

What this means, in non-formal terms, is that if I put one triangle on top of the other, including arranging the top one by flipping it over or rotating it, or both, they will completely overlap.

So these two triangles are also congruent (I rotated the bottom right triangle clockwise):

rotated congruent triangles

And so are these, where I flipped the top left triangle vertically:

flipped congruent triangles

There are three postulates that define when two triangles are congruent.

1. Side-Side-Side: The first postulate is that if two triangles have three sides that are equal, the triangles are congruent. So, the above two triangles, which have three sides that are the same are congruent. This is often written in shorthand as “SSS”.

2. Side-Angle-Side: The 2nd postulate is that if two triangles have two sides that are equal, and the angle between these two sides is the same, the triangles are congruent. This is often written in shorthand as “SAS”.

SAS congruent triangles

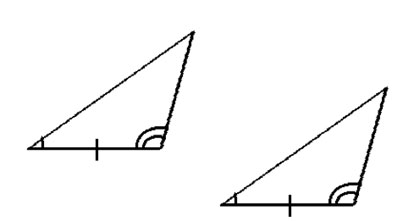
3. Angle-Side-Angle: The 3rd postulate is that if two triangles have one side that is equal, and the angles on both edges of that side are s the same, the triangles are congruent. This is often written in shorthand as “ASA”.

ASA congruent triangles

You will sometimes see a fourth “postulate”, called “angle-angle-side”, which refers to the case of one same side, and two angles which are the same but not on both edges of the same side.

But this is not really a postulate since it can be derived from the previous rules we have. Since we know the sum of angles in any triangle is the same (180°), if two of the angels are the same, the third must also be the same (and equal to 180° minus the sum of the other two angles).

So this “Angle-Angle-Side” postulate is easily shown to be the equivalent to Angle-Side-Angle.

--
Now that we've explained the basic concept of congruent triangles in geometry, let's scroll down to work on specific geometry problems relating to this topic.