Using the known properties of circles, like the fact that their radii are all equal, it is easy to solve geometry problems that require proof that triangles in a circle are congruent. Let’s take a look at one such problem, involving two intersecting circles and the triangles formed by their radii.
Problem
Two circles, with centers O and Q, intersect at points A and B. Prove that △OAQ≅△OBQ.
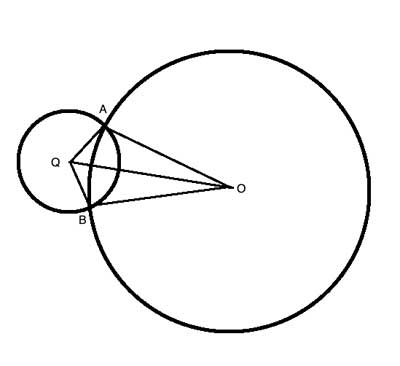
Strategy
One of the sides of these two triangles, the line segment OQ which connects both centers, is common to both triangles. We are not given any information about the angles formed by the radii, so the two postulates of congruent triangles that require angles (Angle-Side-Angle or Side-Angle-Side) seem like less likely options at this point. But what about the third postulate- Side-Side-Side?
The hint as to which other parts we should use to show the congruency is that these triangles were formed by the intersection of two circles- and the other two sides of both triangles are radii of the circles, which are equal to each other, and so we have the needed addiotnal two sides, and the triangles are congruent using the Side-Side-Side postulate.
Proof: congruent triangles in intersecting circles
(1) OQ=OQ //Common side, reflexive property of equality
(2) QA=QB //Both are radii of circle Q, a circle’s radii are equal to each other
(3) OA=OB //Both are radii of circle O, a circle’s radii are equal to each other
(4) △OAQ≅△OBQ //Side-Side-Side postulate.
