The perimeter of any polygon is simply the combined lengths of all its sides. In a polygon like a rectangle or a parallelogram, where the two opposite sides are equal, this can be simply represented as P = length + height + length + height = 2·(length + height)
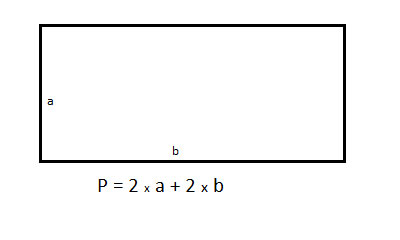
A common problem using the perimeter of a rectangle involves providing the perimeter and one of the sides and asking you to find the other side. This can be done using simple algebra.
Here are a couple of examples.
Problem 1
A rectangle has a perimeter of 100 inches. The longer side is 20 inches longer than the shorter one. Find the length of each side.
Solution
Call the shorter side x. The longer side is x=20. Then:
(1) 100 = 2·(length + height) = 2·(x+x+20)
(2) 50 = 2x+20
(3) 30 = 2x
(4) x=15
So the short side is 15 inches, and the long side is 35 inches.
A slightly more complex problem is the following:
Problem 2
Given a rope of length 100 inches, you can create rectangles with different perimeters. For example: a rectangle with sides measuring 10,10, 40 & 40; or one with sides measuring 20,20,30 & 30. Each rectangle has a different area (the first one in the example has an area of 10x40 or 400 square units; the second one is 20x30=600). What is the rectangle with the largest area you can create with that rope?
Solution
These types of maximization or minimization problems are easily solved using basic calculus techniques - finding the derivative of a function and solving for zero. But this problem is simple enough to solve without requiring any knowledge of calculus.
The area of a rectangle is (length x height). If we have a fixed perimeter of 100, and the perimeter is 2·(length + height), then (length + height) =50.
If we call one side x, the two sides can be represented as x and (50-x). The area of any rectangle we make form this rope is then A=x·(50-x), or A=50x-x2.
From our knowledge of quadratic functions, we know that A=50x-x2 is a parabola with a maximum occurring at x=-50/-2=25, so the largest rectangle is one in which the sides are 25 and 50-25=25 - a square! That square has an area of 625 square units.
