The perimeter of a polygon is the combined length of all its straight-line sides. In many geometry problems, we are asked to find the perimeter of an irregular shape, where not all of the side lengths are given, in many cases, we can use the properties of simple polygons like triangles or rectangles to find the perimeter of such irregular polygons, as in this example.
Problem
Find the perimeter of the following shape, created by cutting a triangle from a square with side 5 units, as in the following drawing.
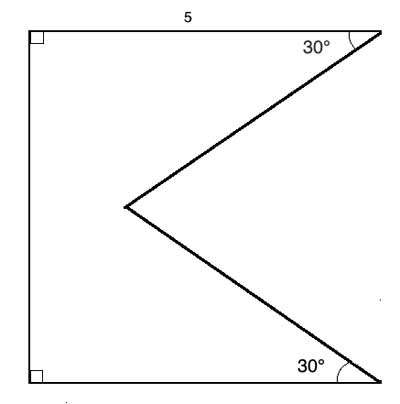
Strategy
The irregular shape was created by taking a square, where all four sides are equal, and replacing one of the sides. Since the original shape was a square, the three sides that remain of the original shape are all equal and measure 5 units each.
The hint for finding out the two other sides is in the given angle - 30 °. In the original shape, which is a square, the interior angles all have a measure of 90°. so if we draw back the missing side of the square, the resulting triangle will have two angles measuring 60°. But if two of the triangle's angles are 60°, then by the sum of angles in a triangle, the third angle must also measure 60° (180° - 60°-60°=60°).
So this triangle is an equilateral triangle, and all its sides have equal length. The missing side which we drew back measures 5 units, since it was originally a side of a square with side length 5 units, and so all sides of the equilateral triangle must also measure 5 units.
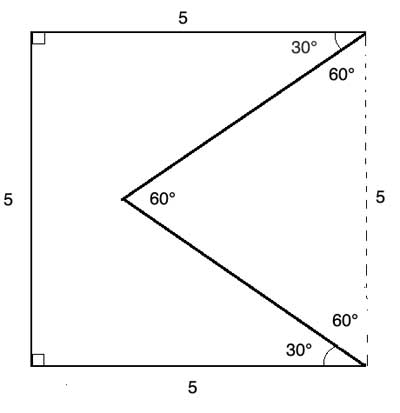
So the perimeter is 5+5+5+5+5=25 units.
