Today we’ll find the angles of a triangle formed by two tangent lines to a circle using inscribed angles, and theorems about the sum of angles in a polygon.
In this geometry problem, we will combine several theorems in order to arrive at the solution:
- Two tangent theorem
- Inscribed angle theorem
- Sum of angles in a triangle theorem
- Sum of angles in a quadrilateral theorem
Problem
A triangle ΔBCD is inscribed in a circle such that m∠BCD=75° and m∠CBD=60°. Show that the triangle ΔABC formed by two tangent lines from point A outside the circle to points B and C is a 45-45-90 Right Triangle.
Strategy
We are given two of the three angles of triangle ΔBCD, so it is easy and usually useful to get the third angle, using the sum of angles in a triangle theorem. We do that to find that m∠BDC=45°.
We’ve also previously said that most problems involving a polygon inscribed in a circle will make use of the inscribed angle theorem, so let’s draw the corresponding central angle to ∠BDC, ∠BOC, and using the inscribed angle theorem know it measures 90°.
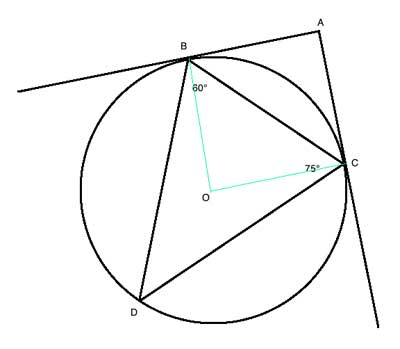
Since AB and AC are tangent lines to the circle, they are perpendicular to the radii OB and OC at the points B and C, so in quadrilateral ABOC we have three angles that measure 90° each, and the remaining angle ∠BAC must be 90° as well since the sum of angles in a quadrilateral is 360°.
Finally, from the two tangent theorem, we know that AB=AC, so ΔABC is an isosceles triangle, and by the base angle theorem, m∠ABC=m∠ACB, so they each must be 45°.
Solution
(1) m∠BCD=75° //Given
(2) m∠CBD=60° //Given
(3) m∠BDC=45° //(1) , (2) , Sum of angles in a triangle
(4) m∠BOC=90° //(3), inscribed angle theorem
(5) m∠ABO=90° //Given, AB is tangent to O
(6) m∠ACO=90° //Given, AC is tangent to O
(7) m∠BAC=90° //(4) ,(5), (6), Sum of angles in a quadrilateral
(8) AB=AC //Two tangent theorem
(9) m∠ABC=m∠ACB //(8), base angle theorem
(10) m∠ABC=m∠ACB=45° //(7),(9), Sum of angles in a triangle
And so we have found the angles of a triangle formed by two tangent lines to a circle using inscribed angles.
