This theorem states that if we draw two lines from the same point which lies outside a circle, such that both lines are tangent to the circle, then their lengths are the same. We will now prove that theorem.
Problem
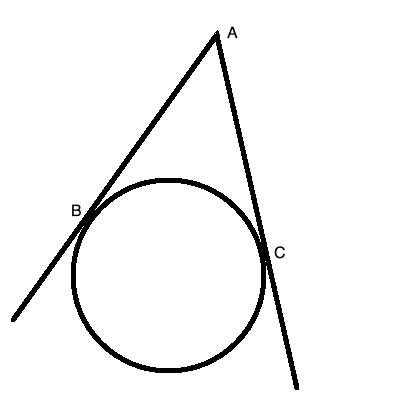
AB and AC are tangent to circle O. Show that AB=AC
Strategy
To show two lines are equal, a helpful tool is triangle congruency. The shape of the drawing in the problem statement - where the two tangent lines create a sort of triangular 'clown's hat' also suggests we would be served by constructing some triangles here, where the two tangent lines are sides.
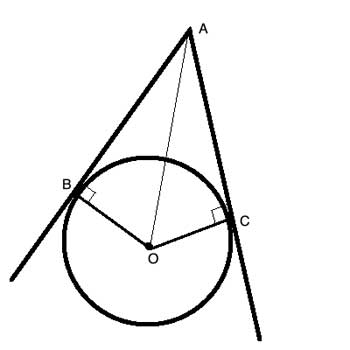
We also know that a property of the tangent lines to a circle is that they form a 90° angle between the line and a radius at the point of tangency - so let's draw that:

And now the triangles almost present themselves. Connect the point A with a line segment to the center of the circle, O, and we will have two right triangles, with a common hypotenuse (AO), and an equal leg, as both radii are equal, and the triangles are congruent by HL.
Proof
(1) AB is tangent to Circle O //Given
(2) ∠ABO=90° //tangent line is perpendicular to circle
(3) AC is tangent to Circle O //Given
(4) ∠ACO=90° //tangent line is perpendicular to circle
(5) AO=AO //common side (reflexive property)
(6) OC=OB=r //radii of a circle are all equal
(7) △ABO≅△ACO //Hypotenuse-leg
(8) AB=AC // Corresponding sides in congruent triangles (CPCTC)
This theorem is a key element in proving the Pitot Theorem, about a quadrilateral that circumscribes a circle.
