A tangential quadrilateral is a quadrilateral whose four sides are all tangent to a circle inscribed within it. In such a quadrilateral, the sum of lengths of the two opposite sides of the quadrilateral is equal.
This is known as the Pitot theorem, named after Henri Pitot, a French engineer who proved it in the 18th century.
Problem
A circle is inscribed in a quadrilateral ABCD. Show that |AB|+|CD| = |BC|+|DA|

Strategy
We are working with a tangential quadrilateral, so all the sides are tangent to the circle. Let's review the properties of tangents to a circle.
One of the theorems we have proved is the two tangent theorem - two tangents from the same point outside a circle have equal lengths to the points of tangency. This should be useful here, as it deals with the lengths of such tangents.
Looking at the quadrilateral, we have four such points outside the circle. Each one of the quadrilateral's vertices is a point from which we drew two tangents to the circle.
Applying the two tangent theorem to each one of these points, we get 4 pairs of equal-size line segments: AP=AS=a; BP=BQ=b; CQ=CR=c and DR=DS=d.
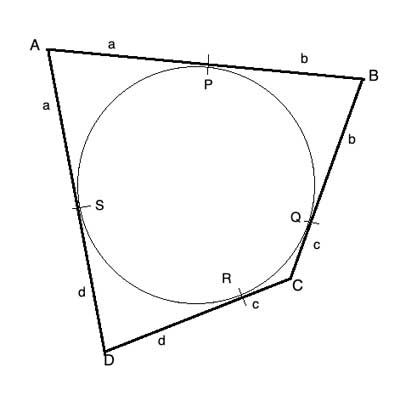
And in each of the opposite pairs of sides of the quadrilateral, we have exactly one of these segments, so their sums are equal. And we have proven the Pitot theorem for a circle inscribed in a quadrilateral.
Proof
(1) AP=AS=a // Two tangent theorem
(2) BP=BQ=b // Two tangent theorem
(3) CQ=CR=c // Two tangent theorem
(4) DR=DS=d // Two tangent theorem
(5) |AB|+|CD| = |AP|+|PB|+|CR|+|RD|= a+b+c+d
(6) |BC|+|DA| = |BQ|+|QC|+|DS|+|SA|=b+c+d+a=a+b+c+d // Commutative property of addition
(7) |AB|+|CD| = |BC|+|DA| //(5),(6), transitive property of equality
