Area of Geometric Shapes

The area of a geometric shape is a property that describes how much space it takes up.

Regular geometric shapes like circles, parallelograms and triangles have simple formulas that give their area.

The area of irregular shapes can sometimes be computed by reducing it into several regular shapes.

Some common area formulas:

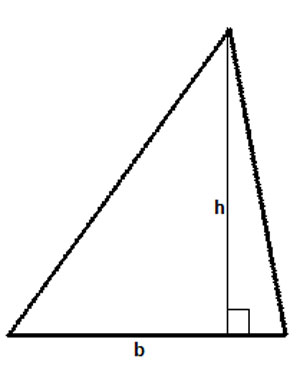
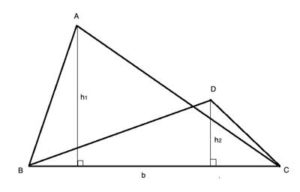
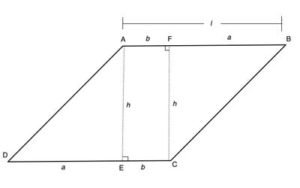
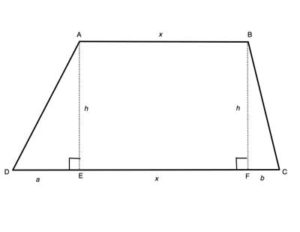
For triangles: Area = (h x b) /2

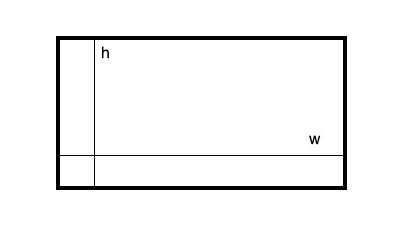
For rectangles: Area = h x w

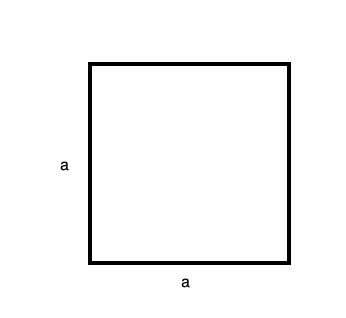
Since a square is a special type of rectangle, its area is given by the same formula. But since in the square's case the width is the same as the hight, this becomes Area = a x a = a²

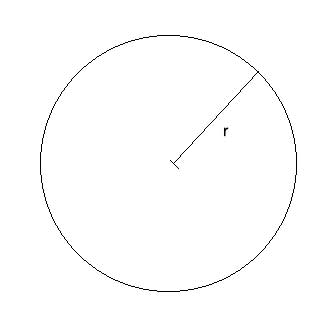
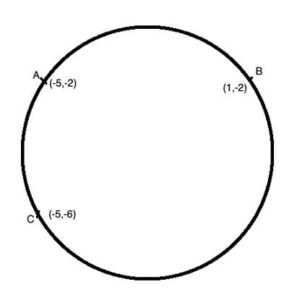
A circle's area is given by the formula A_circle=π*r²

--
Now that we've explained the basic concept of area in geometry, let's scroll down to work on specific geometry problems relating to this topic.