A Square and an Equilateral Triangle, in a Circle

In this problem we have an equilateral triangle on top of a square, in a circle, and we need to find the area of the circle, using the length of the side of the square.

This problem has a number of variations in geometry textbooks - sometimes the area of the square is given , and we can find the length of its side from that (using the formula for an area of a square : Area = a x a = a², so a=√ Area) . In other problems, we are given the square's perimeter (in which case the side is a=P/4) or the triangle's perimeter (in which case the side is a=P/3).

We can even find the length of the side a from the triangle's height or its area (relying on the fact that the height of an equilateral triangle bisects the apex angle, creating a 30-60-90 right triangle).

Problem

An equilateral triangle sits on top of a square with a side measuring 10 units. A circle passes through the vertices of the square and the triangle which are not shared, as in the drawing:

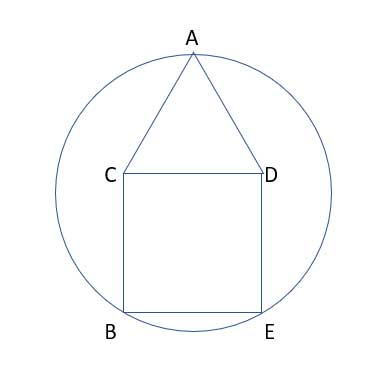
Find the area of the circle.

Strategy

The first step is to find the lengths of all the sides, with the insight that an edge of the triangle is equal to an edge of the square, since all sides of the square are equal and all side of an equilateral triangle are equal, and they share a common side (CD).

So |AC|=|CB|=|BE|=|ED|=|DA|=10.

And as explained in the intro paragraph, above, we could also do this if instead of the side of the square have its area, or perimeter, or the perimeter of the triangle or the triangle's height or area.

Also, note that m∠ACD=60^∘ (as an angle of an equilateral triangle), and m∠DCB=90^∘ (as an angle of the square), so m∠ACB=150^∘, by the Angle Addition Postulate.

Next, to find the area of a circle we need its radius, so let's draw that radius. Actually. let's draw a few of them:

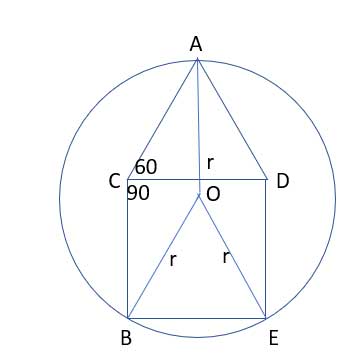
Now from here, we have several ways of finding out r from the given sides and some angle math.

Method 1: Show that ΔOBE is equilateral

We immediately see that ΔOBE is isosceles, since |OB|=|OE|=r (they are both radii of the circle). So if we show one of its angles measures 60^∘, it is also equilateral, and then r=|BE|=10. To do this, let's draw a couple of additional lines, AB and AE:

ΔACB is isosceles, with |AC|=|CB|=10, from above. m∠ACB=150^∘ as we have shown earlier, so m∠CAB=m∠CBA=(180^∘-150^∘)/2=15^∘. And similarly, for the other triangle: ΔADE is isosceles, with |AD|=|DE|=10, from above. m∠ADE=150^∘ for similar reasons as we have shown earlier, so m∠DAE=m∠DEA=(180^∘-150^∘)/2=15^∘.

Angles ∠CBE and ∠DEB are both right angles, as angles of the square, and so both measure 90^∘. Some angle math gives us m∠ABE=m∠CBE-m∠CBA= 90^∘-15^∘=75^∘, and also m∠AEB=m∠DEB-m∠DEA= 90^∘-15^∘=75^∘. so m∠ABE=m∠AEB, and ΔAEB is isosceles, by the Converse Base Angle Theorem, and AB=AE. And we also have m∠BAE=30^∘, as the third angle of isosceles triangle ΔAEB with base angles of 75^∘.

Now let's consider the two triangles, ΔABO and ΔAEO. AB=AE, as we have just shown, OB=OE=r, and AO=AO as a common side, so they are congruent by the Side-Side-Side postulate. From this, we have ∠BAO≅∠EAO as corresponding angles in congruent triangles.

m∠BAO=m∠EAO, and m∠BAO+m∠EAO=m∠BAE=30^∘, so m∠BAO=m∠EAO=15^∘. And since ΔAOB is isosceles (|AO|=|OB|=r), m∠BAO=m∠ABO=15^∘

Going back to m∠ABE=75^∘, we now have m∠OBE=m∠ABE-m∠ABO=75^∘-15^∘=60^∘. ΔOBE is thus an equilateral triangle (it is isosceles with |OB|=|OE|=r, and has one angle of 60^∘), and r=|OB|=|BE|=10.

And the circle's area is thus A_circle=π*r²=π*10²=100π

Let's write the proof formally, so we'll be able to use what we have shown here in the next two methods.

Proof

(1) |CB|=|BE|=|ED|=|DC|=10 //Sides of square are equal, side is given as 10
(2) |DC|=|CA|=|AD|=10 //Side of equilateral triangle are equal, (1)
(3) m∠ACD=60^∘ //angles of an equilateral triangle all measure 60^∘
(4) m∠DCB=90^∘ //angles of a square all measure 90^∘
(5) m∠ACB=m∠ACD+m∠DCB=60^∘+90^∘=150^∘ //Angle Addition Postulate
(6) |AC|=|CB|=10 //(1), (2)
(7) m∠CAB=m∠CBA=(180^∘-150^∘)/2=15^∘ //(6), Base Angles Theorem
(8) m∠ADC=60^∘ //angles of an equilateral triangle all measure 60^∘
(9) m∠CDE=90^∘ //angles of a square all measure 90^∘
(10) m∠ADE=m∠ADC+m∠CDE=60^∘+90^∘=150^∘ //Angle Addition Postulate
(11) |AD|=|DE|=10 //(1), (2)
(12) m∠DAE=m∠DEA=(180^∘-150^∘)/2=15^∘ //(11) , Base Angles Theorem
(13) m∠CBE =m∠DEB = 90^∘ //angles of a square all measure 90^∘
(14) m∠ABE=m∠CBE-m∠CBA= 90^∘-15^∘=75^∘ //(13),(7)
(15) m∠AEB=m∠DEB-m∠DEA= 90^∘-15^∘=75^∘ //(13), (12)
(16) m∠ABE=m∠AEB //(14), (15), transitive property of equality
(17) AB=AE //(16) , Converse Base Angle Theorem
(18) m∠BAE=180^∘-(75^∘+75^∘) = 30^∘ //(16), Apex angle of isosceles triangle with base angles of 75^∘
(19) OB=OE=r //radii of a circle are all equal
(20) AB=AE //(17)
(21) AO=AO //Common side
(22) ΔABO ≅ΔAEO //(20), (21) , (19), Side-Side-Side postulate.
(23) ∠BAO≅∠EAO //Corresponding angles of congruent triagles (CPCTC)
(24) m∠BAO=m∠EAO //(23), definition of congruent angles
(25) m∠BAO+m∠EAO=m∠BAE=30^∘//(18), Angle Addition Postulate
(26) m∠BAO=m∠EAO=15^∘ //(24), 25)
(27) |AO|=|OB|=r //radii of a circle are all equal
(28) m∠BAO=m∠ABO=15^∘ //(27), (26), Base angle theorem and transitive property of equality
(29) m∠OBE=m∠ABE-m∠ABO=75^∘-15^∘=60^∘ //(14), (28), Angle Addition Postulate
(30) m∠OBE=m∠OEB =60^∘ //(19), Base angle theorem
(31) m∠BOA =60^∘ //(30), Sum of angles in triangle is 180^∘
(32) |OB|=|BE|=10=r //(1), (30), (31), ΔOBE is equilateral
(33) A_circle=π*r²=π*10²=100π //(32)

Method 2: Show that ΔACB and ΔAOB are congruent

Triangle ΔAOB has two sides which are the circle's radii, and ΔACB has two sides which are known. So if we show they are congruent, we will have the length of the radius.

Relying on what we proved in Method 1, we have m∠CAB=m∠CBA=(180^∘-150^∘)/2=15^∘, and also m∠BAO=m∠ABO=15^∘. AB is a common side, so ΔACB ≅ΔAOB, using the Angle-Side-Angle postulate. And from this it follows that |AC|=|AO|=r=10, and we are done.

Proof

(34) m∠CAB=m∠CBA=(180^∘-150^∘)/2=15^∘ //(7)
(35) m∠BAO=m∠ABO=15^∘ //(28)
(36) AB=AB //common side, reflexive property of equality
(37) ΔACB ≅ΔAOB // Angle-Side-Angle postulate
(38) |AC|=|AO|=r //Corresponding sides of congruent triangles (CPCTC)
(39) |AC|=10 //(2)
(40) A_circle=π*r²=π*10²=100π //(39)

Method 3: Show that AO is perpendicular to CD

If AO⊥CD, then AO||CB. Then , relying on what we have shown above - m∠CAB=m∠ABO=15^∘, and AC||OB. So AOBC is a parallelogram, and |AC|=|OB|=r, as opposite sides of a parallelogram.

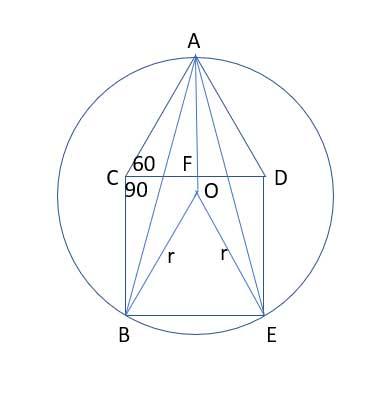
(41) m∠ACD=60^∘ //angles of an equilateral triangle all measure 60^∘
(42) m∠CAB=15^∘ //(7)
(43) m∠BAO=15^∘ //(28)
(44) m∠CAO=m∠CAB+m∠BAO = 15^∘+15^∘=30^∘ //Angle addition postulate
(45) m∠CAF= 180^∘-m∠CAO-m∠ACD=180^∘-30^∘- 60^∘= 90^∘ //(41), (44) , sum of angles in triangle ΔCAF
(46) AO⊥CD //(45), definition of perpendicular lines
(47) m∠DCB=90^∘ //angles of a square all measure 90^∘
(48) AO||CB //(47), (45), Converse Alternate Interior Angles Theorem
(49) m∠ABO=15^∘ //(28)
(50) AC||OB //(42), (49), Converse Alternate Interior Angles Theorem
(51) AOBC is a parallelogram //definition of a parallelogram
(52) |AC|=|OB|=r //Opposite sides of a parallelogram are equal
(53) |AC|=10 //(2)
(54) A_circle=π*r²=π*10²=100π //(52), (53)