A 30-60-90 triangle is a right triangle with angles that measure 30 degrees, 60 degrees, and 90 degrees. It has some special properties. One of them is that if we know the length of only one side, we can find the lengths of the other two sides.
Problem
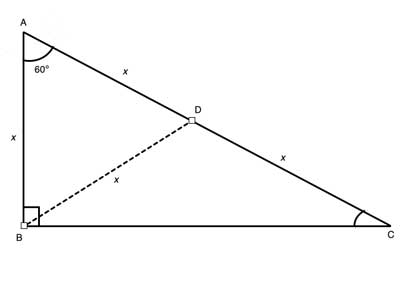
In a right triangle ΔABC, m∠CAB=60°, the length of leg AB is x. Find the length of the other leg and the hypotenuse, in terms of x.
Strategy
The 60° angle is a hint to use the properties of an equilateral triangle. Recall that in a right triangle, the median to the hypotenuse is equal to half the hypotenuse, and creates two isosceles triangles.
In this case, since the isosceles triangle ΔDAB has one base angle which is 60° (∠DAB), the other base angle (∠DBA) is also 60°, and so the remaining angle (∠ADB) must also be 60°, and we have an equilateral triangle.
So if AB=x, AD is also equal to x. And since the median to the hypotenuse is equal to half the hypotenuse, AC=2x. And we can now use the Pythagorean theorem to find the length of the remaining leg BC.
Solution
(1) AD=DC //Construction
(2)m∠ABC=90° //Given, ΔABC is a right triangle
(3)BD=DA //the median to the hypotenuse is equal to half the hypotenuse
(4) m∠CAB=60° // Given
(5) m∠DBA=60° // (3), (4), Base angles of an isosceles triangle are equal
(6) m∠ADB=60° // (4), (5) Sum of angles in a triangle is 180°
(7) AD=AB=x // sides of an equilateral triangle are all equal
(8) AC=2x //the median to the hypotenuse is equal to half the hypotenuse
(9) AC2=AB2+BC2 //Pythagorean theorem
(10) (2x)2=x2+BC2
(11) 4x2=x2+BC2
(12) 3x2=BC2
(13) BC=x·√3
So we found that in a 30-60-90 triangle, if the short leg is x, the hypotenuse is 2x and the long leg is x·√3.
Given this relationship, if we know the hypotenuse, we can find the two legs (the short leg is hypotenuse/2 and the long leg is the short leg times √3. ); and if we know the long leg, we can find the short leg (long leg divided by √3) and the hypotenuse (short leg times two).
And this is how, In a 30-60-90 triangle, if we know the length of only one side, we can find the lengths of the other two sides.
