We can use the properties of an equilateral triangle and a 30-60-90 right triangle to find the area of a circle inside an equilateral triangle, using only the triangle's side length.
Problem
An equilateral triangle has side length x. Find the circle's area in terms of x.
Strategy
We know a circle is fully defined by the length of its radius, r, so the key here will be to find that - the length of segment OD.
There are several quick ways to find that length which rely on properties of the centroid - the point where all three medians of the triangle meet. The centroid of an equilateral triangle lies on the medians, which are also perpendicular to the bases, and splits the medians into two segments measuring ⅓ of the length and ⅔ of the length, respectively.
But to prove those properties of the centroid (like the fact that all three medians do in fact meet at one point, or that the centroid is also the center of the circle) is quite complex and beyond the scope of high school geometry.
So instead, I will use a longer process, that only relies on things we have already proven using triangle congruency.
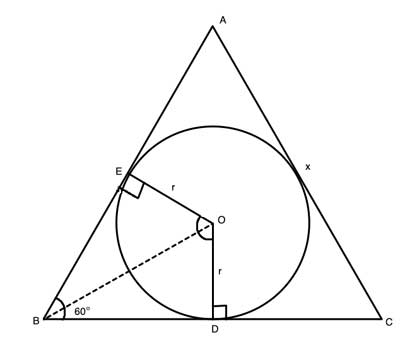
The sides of the triangle are tangent to the circle, so the two radii, OE and OD, are perpendicular to the sides of the triangle (AB and BC), and are equal to each other. BE=BD, using the Two Tangent theorem.
BEOD is thus a kite, and we can use the kite properties to show that ΔBOD is a 30-60-90 triangle. Then, if we find the length of one of its sides, we can find all three sides, including OD.
By showing the congruency of triangles ΔBOD and ΔCOD, we'll find that BD is half of BC and equal to x/2, OD will then be (x/2)/√3, and we are done.
Proof
(1) OE = OD = r //radii of a circle are all equal to each other
(2) BE=BD // Two Tangent theorem
(3) BEOD is a kite //(1), (2) , defintion of a kite
(4) m∠ODB=∠OEB=90° //radii are perpendicular to tangent line
(5) m∠ABD = 60° //Given, ΔABC is equilateral
(6) m∠OBD = 30° // (3) In a kite the diagonal bisects the angles between two equal sides
(7) ΔBOD is a 30-60-90 triangle //(4), (5), (6)
(8) r=OD=BD/√3 //Properties of 30-60-90 triangle
(9) m∠OCD = 30° //repeat steps (1) -(6) for triangle ΔOCD, symmetry
(10) ∠OCD≅∠OBD //(6),(9)
(11) ∠DOB≅∠DOC //(10), (4), sum of angles in a triangle
(12) OD=OD // common side, reflexive property of equality
(13) ΔBOD≅ΔCOD //Angle-side-Angle postulate
(14) BD=CD=x/2 //Corresponding sides in congruent triangles (CPCTC)
(15) OD=(x/2)/√3 //(8), substitution
(16) Areacircle=πr2
(17) Area = π[(x/2)/√3]2
(18) Area = πx2/12
