A scalene triangle is a triangle in which all three sides have different lengths. The scalene inequality theorem states that in such a triangle, the angle facing the larger side has a measure larger than the angle facing the smaller side.
Problem
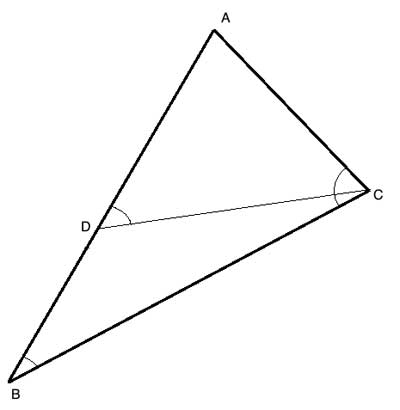
In scalene triangle ΔABC, AB>AC. Show that m∠ACB> m∠ABC
Strategy
We have one theorem that tells us when angles in a triangle are equal - the Base Angles Theorem, and one postulate that tells us when one angle is larger than another - the Angle Addition Postulate.
Let's try to combine these two things: to use the Base Angles theorem, we'll construct an isosceles triangle. Since we know AB>AC, we'll find a point D, on side AB, such that AD=AC.
From the Base Angles theorem, we know ∠ADC≅ ∠ACD, and so m∠ADC= m∠ACD. But as D is an interior point to angle ∠ACB, from the angle addition postulate we know that m∠ACB = m∠ACD+m∠DCB, and so m∠ACB > m∠ACD and so m∠ACB > m∠ADC. But ∠ADC is an exterior angle to triangle ΔDBC, and so is equal to the sum of the two remote interior angles.
So if m∠ADC=m∠DBC+m∠DCB, m∠ADC>m∠DBC. Combining this with m∠ACB > m∠ADC we get m∠ACB > m∠ABC
Proof
(1) AB>AC //Given
(2) AD=AC //Construction
(3) ∠ADC≅ ∠ACD //Base Angles theorem
(4) m∠ADC= m∠ACD // Defintion of congruent angles
(5) m∠ACB = m∠ACD+m∠DCB // Angle addition postulate
(6) m∠ACB > m∠ACD //(5), m∠DCB is positive
(7) m∠ADC=m∠DBC+m∠DCB //Exterior angle theorem
(8) m∠ADC>m∠DBC //(7), m∠DCB is positive
(9) m∠ACB > m∠ACD=m∠ADC>m∠DBC //(6), (4), (8)
(10) m∠ACB > >m∠ABC //transitive property of inequality
