Lines and Angles

Lines and angles are two of the most basic elements of geometry.

What is a line?

A line is an abstract concept. It has no width, only length, and that length is infinite in both directions. A part of a line that is bounded by two points is called a line segment. One of the formal definitions of a line is that it is the collection of all points that are the same distance from two other points on a plane:

The segment addition postulate states that if we have a line segment defined by two points, A and C, a third point , B, is on the same line if (and only if) the length of segment AB plus the length of segment BC is equal to the length of AC:

|AB|+|BC|=|AC|

Angles

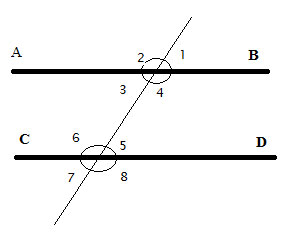
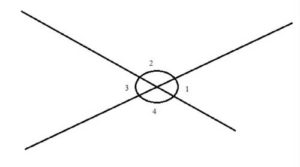
When 2 lines or line segments intersect, they form angles:

We measure angles in units called degrees, and marked with a °, where a full circle is 360°.

--
Now that we've briefly explained the basic concept of lines and angles in geometry, let's scroll down to the post below that explains these concepts more in depth. For specific geometry problems in the area of lines and angles, check out the following links:
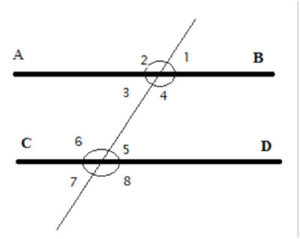
Intersecting Lines and Angles
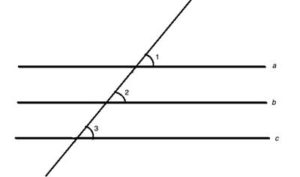
Parallel Lines
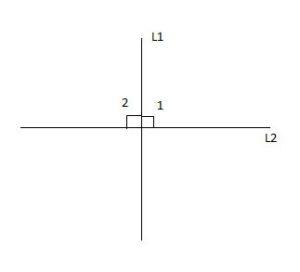
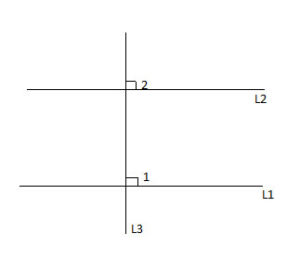
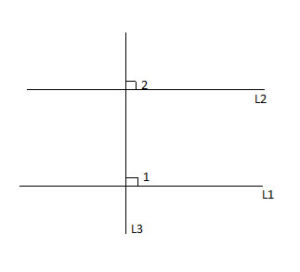
Perpendicular Lines

Parallel Lines are Equidistant

Consecutive Interior Angles Converse Theorem

Three Parallel Lines Theorem

Converse of the Angle Bisector Equidistant Theorem

Angle Bisector Equidistant Theorem

Intercept Theorem

Two Lines Parallel to a Third are Parallel to Each Other

Converse Alternate Interior Angles Theorem

Shortest Distance Theorem

Lines and Angles

Linear Pair Perpendicular Theorem

Converse of the Corresponding Angles Theorem

Alternate Interior Angles Theorem

Consecutive Interior Angles Theorem

Vertical Angles Theorem

Perpendicular Transversal Theorem

Converse Perpendicular Transversal Theorem