In today's lesson, we will show how to prove the converse of the Angle Bisector Equidistant Theorem.
The Angle Bisector Equidistant Theorem states that any point that is on the angle bisector is an equal distance ("equidistant") from the two sides of the angle.
The converse of this is also true. If a point lies on the interior of an angle and is equidistant from the sides of the angle, then a line from the angle's vertex through the point bisects the angle. Let's see how we prove it.
Problem
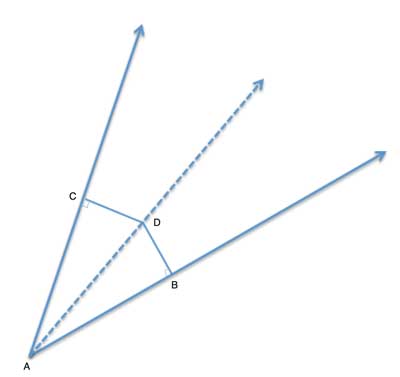
D is a point in the interior of angle ∠BAC. The perpendicular distances |DC| and |DB| are equal. Show that AD is the angle bisector of angle ∠BAC (∠BAD≅ ∠CAD).
Strategy
The converse of the Angle Bisector Equidistant Theorem is not difficult to prove. In fact, it's as easy to prove as the original theorem, once again using congruent triangles.
When you are asked to prove a converse theory to a theory that you have just proved, it is often a good idea to follow the same strategy as in the original proof, simply switching what needs to be proven with what is already given.
So in this case, △ABD and △ACD share a common side (AD), have another pair of sides which is given as equal (|DC| = |DB|), and both are right triangles - so they are congruent right triangles using the hypotenuse-leg postulate.
It follows that the line AD is the bisector as the angles ∠BAD and ∠CAD are congruent as corresponding parts of congruent triangles. See? That was fairly easy!
Proof
(1) AD=AD //Common side, reflexive property of equality
(2) |DB|=|DC| //Given
(3) m∠DCA=m∠DBA=90° //definition of distance.
(4)△ABD≅△ACD //(2),(3), Hypotenuse-Leg Postulate
(6) ∠BAD≅ ∠CAD //Corresponding sides of congruent triangles (CPCTC)