In today's geometry lesson, we will show a fairly easy way to prove the perpendicular bisector theorem.
A line that splits another line segment (or an angle) into two equal parts is called a "bisector." If the intersection between the two line segment is at a right angle, then the two lines are perpendicular, and the bisector is called a "perpendicular bisector".
The Perpendicular Bisector Theorem states that a point on the perpendicular bisector of a line segment is an equal distance from the two edges of the line segment.
Problem
Point C is on the perpendicular bisector of segment AB. Prove that |CA|=|CB|
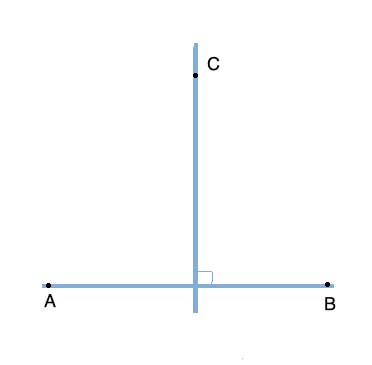
Strategy
We need to prove two line segments are equal, so let's draw them:
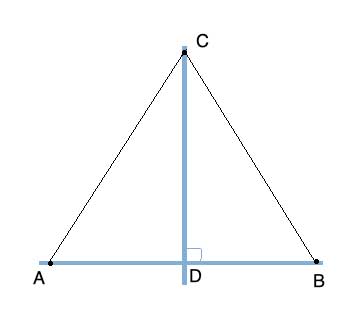
And now it should be clear that the way to go here is to use congruent triangles. We have a common side (CD). We also have two segments given as equal (AD=DB) since AD is the bisector. And we have an equal angle, which is a right angle, in between them.
Proof
(1) CD=CD //Common side, reflexive property of equality
(2) AD=DB //Given, CD is a bisector
(3) m∠ADC= m∠BDC =90° //Given, CD is perpendicular to AB
(4) ∠ADC≅ ∠BDC //Side-Angle-Side postulate
(5) CA=CB //corresponding sides of congruent triangles (CPCTC)
And so we have proved the Perpendicular Bisector Theorem. Note that this is a converse theorem to one of the properties of an isosceles triangle - that the median to the base (which is a bisector) is perpendicular to the base. Here we prove the opposite - if we have a perpendicular median, the triangle is isosceles.