In a triangle, a line that connects one corner (or vertice) to the middle point of the opposite side is called a median. A property of isosceles triangles, which is simple to prove using triangle congruence, is that in an isosceles triangle, the median to the base is perpendicular to the base.
Problem
Show that in an isosceles triangle ΔABC, the median to the base, AD, is perpendicular to the base.
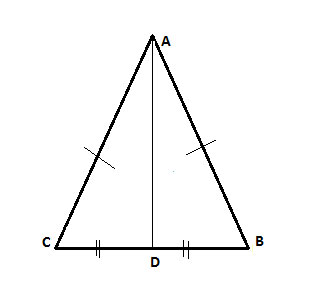
Strategy
We will again work backward from what we need to ultimately show. To prove that two lines are perpendicular to each other, we need to show that the angle between them is 90°.
One tool that helps us show that an angle is 90° is the Linear Pair Perpendicular Theorem - if two straight lines intersect at a point and form a linear pair of equal angles, they are perpendicular.
This is great, since triangle congruence can show that angles are equal. And here, proving that triangles are congruent is almost too easy! All the sides are given as equal, so the triangles are congruent using the Side-Side-Side postulate.
Proof
(1) ΔABC is isosceles //Given
(2) AD is the median to the base, AB //Given
(3) AD=AD //Common side
(4) AB=AC //(1), definition of isosceles triangle
(5) BD=DC //(2), definition of median
(6) △ABD≅△ACD // Side-Side-Side postulate.
(7) ∠ADB ≅ ∠ADC // Corresponding angles in congruent triangles (CPCTC)
(8) AD⊥BC // Linear Pair Perpendicular Theorem
